12.1 Invent. Create. Enjoy!

Exploding Dots

12.1 Invent. Create. Enjoy!

Course Home

The lovely thing about Exploding Dots is that it provides a space int invent, create, and play! This is the nature of true joyous mathematics.

Here we give some snippets of ways students and adults from all around the world are creating and inventing with Exploding Dots. Share your inventions and ideas with me using this contact link. (If you have attachments, let me know.)

Goldfish & Robin and friends have some fun advice on some ways to create and play with Exploding Dots.

Let’s make this a growing, community page of global play!

This page is just starting. More will come as more is submitted!

Taking Dots into the Second Dimension

People are playing with two-dimensional arrays of squares.

Goldfish & Robin see the crazy \(2 \leftarrow 3\) machine as a diagonal.

Here are some more thoughts on the matter and their much deeper video on all this – and more – appears here.

Kiran B. has been playing in this direction too, but for two-variable polynomial division

and for solving simultaneous equations.

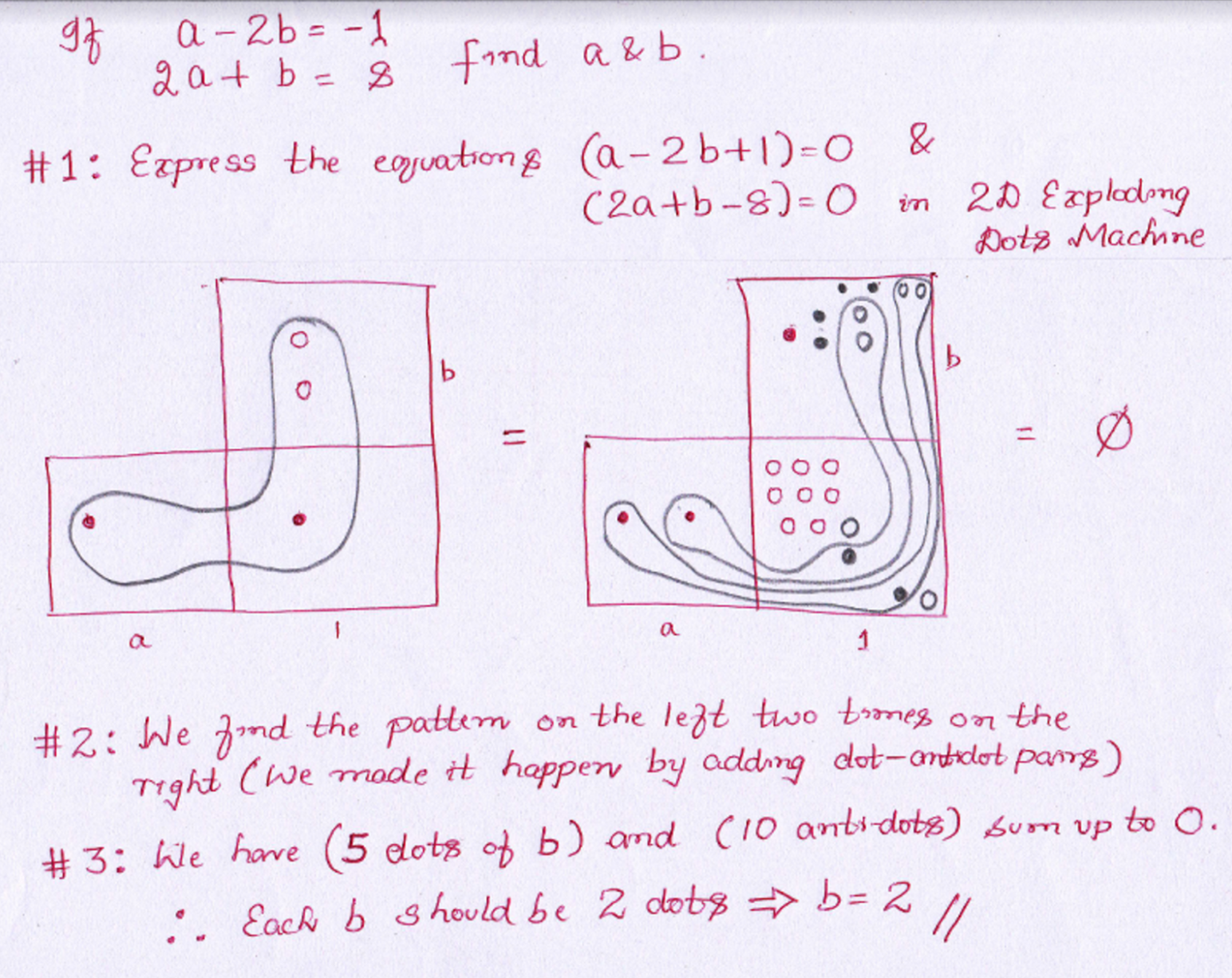
He’s written about this work too in a blog post.

He has since started playing with expressions of the form \(a+\sqrt{b}\) via two-dimensional arrays too: Kiran 2D_ExplodingDots_PascalTriangle .

And why stay with square arrays? Goldfish and Robin are playing with multiplicative patterns in triangular arrays.

Other Models for Exploding Dots

Why not use disappearing cards or smash cheese balls as or eat berries to demonstrate Exploding Dots machines?

Going back into the Past

Can one make sense of the Roman numeral system via Exploding Dots? Sure!

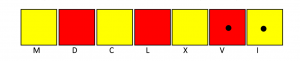Kiran B. explains his work here.

And sometimes people realise they are discovering the same math in different ways! The triangle grid approach is the same interleaving idea.

Actually build a machine!

Glen Whitney of mathwalks.org did! See it in action here.

Surprising Connections

After reading the chapter on polynomial division, mathematics Professor Richard Hoshino, author of The Math Olympian, shared the following with Ambassadors of the Global Math Project:

Inspired by what I read today, I spent a few hours at a coffee shop playing with Exploding Dots. From this super-creative session, I wanted to share two fun problems that you and your students might enjoy based on the last chapter of James’ text.

(1) James defines a \(1|0|0 \leftrightarrow 0|1|1\) machine and explains why this is equivalent to a \( 1 \leftarrow \phi\) machine, where \(\phi\) is the golden ratio \(\left(1+\sqrt(5)\right)/2\). I was interested in seeing what positive integers had “machine” representations with as few 1s as possible, and which positive integers had representations with as many 1s as possible. Let \(f(n)\) be the “phi-nary” representation of \(n\). I noticed a particularly shocking pattern:

f(2) = 10.01,

f(3) = 100.01,

f(7) = 10000.0001,

f(18) = 1000000.000001,

f(47) = 100000000.00000001

f(1) = 1,

f(4) = 11.1111,

f(11) = 1111.111111,

f(29) = 111111.11111111,

f(76) = 11111111.1111111111

Let’s look at all the integers \(n\) for which \(f(n)\) is either all 1’s, or consists of only 1s at the ends. We get the sequence \(\{2, 1, 3, 4, 7, 11, 18, 29, 47, 76, \dots\}\). This is known as the Lucas sequence, i.e., the Fibonacci sequence with starting terms 2 and 1. Beautiful, eh?

Question: prove that \(n\) has one of these two special “phi-nary” representations if and only if \(n\) is a Lucas number.

(2) In 1996, as a high school senior, I wrote the United States of America Mathematical Olympiad (USAMO), arguably a harder math contest than the International Mathematical Olympiad (IMO). The last question of the 1996 paper is as follows:

Determine (with proof) whether there is a subset \(X\) of the integers with the following property: for any integer \(n\) there is exactly one solution of \(a+2b=n\) with \(a\) and \(b\) both belonging to set \(X\).

The majority of us (me included) got shut out on this problem, since it was hard to make progress on this problem. One idea is to attempt to construct some set \(X\) that satisfies the property, starting with small negative and positive numbers. But it’s hard to make progress, given that one needs to rigorously justify that any integer \(n\) can be represented in the form \(a+2b\) in exactly one way.

Here is where the Exploding Dots machine comes to the rescue!

Consider a \(-1 \leftarrow 4\) machine, or what we would think of as “base negative four”. For example, \(111 = (-4)^2 + (-4)^1 + (-4)^0 = 13\). Let \(X\) be the set of integers whose machine representations in “base negative four” consist only of 0s and 1s, with no 2s and 3s. For example, 13 belongs to set \(X\), but 14 does not.

Question: prove that \(X\) is the desired set in the above USAMO question, i.e., for any integer \(n\), there is exactly one way that \(n\) can be written as the sum \(a+2b\), where \(a\) and \(b\) both have only 0s and 1s in every box of the \(-1 \leftarrow 4\) Exploding Dots Machine.

Looking for Palindromes

Dr. Gary Davis writes about fun and cool numerical exploration on his site crikeymath.com. This story on a search for palindromes in a \(2 \leftarrow 3\) machine is intriguing a number of people.

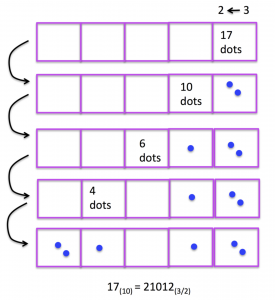
Dr. James Propp writes about it too in his beautiful Mathematical Enchantments column here.

Working with Irrational Bases

Here’s another gem from Kiran B.

Look Into the Past

Professor Stephen Lucas of James Madison University points out that many wonderful ideas are discovered, re-discovered, and emerge in all sorts of ways and variants of ways. One can explore what work was done in the past that matches or ties in with the work we play with today.

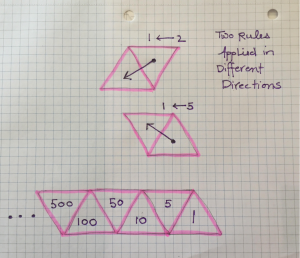
For example, an ancient counting device, a “counting table,” consisted of a flat surface with vertical lines drawn across it. A counter placed on a line represented a power of ten (lines here correspond to boxes in a \(1 \leftarrow 10\) machine), and placing place a counter to the left of a line represented five of that power of ten (to match Kiran B’s interleaving of two machines as above). Arithmetic on these tables was done essentially our Exploding Dots way.

Variants of this design were introduced: The Romans moved the “fives” to the top of the table, rather than to the side of the line, and some historians suggest this led to the Chinese abacus with beads on rods and a horizontal spacer to separate the units from the fives.

Care to research the full history of the abacus?

Also … for two dimensional work, check out “Napier’s Chessboard Abacus.” Martin Gardner wrote about it in Knotted Doughnuts and other mathematical entertainments (W.H.Freeman and Company, 1986).

Division in a \(2 \leftarrow 3\) Machine

Performing division in this weird machine is surprisingly subtle, hard, and mysterious. Here are some thoughts on the matter from Goldfish & Robin. Video