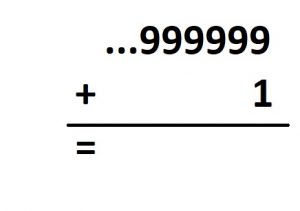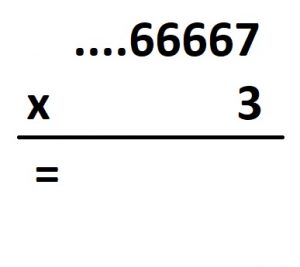Exploding Dots
10.2 A Troubling Number our Usual Mathematics Rejects
Lesson materials located below the video overview.
The number \(0.9999\ldots\) (if you choose to believe it is a one) has infinitely many \(9\)s to the right of the decimal point. What if we consider the “number” with infinitely many \(9\)s to the left of the decimal point instead?
\(\ldots 9999\)
This is a number that ends with nine. Actually it ends with ninety-nine. Actually it ends with nine-hundred-and-ninety-nine. And so on.
Let’s apply our algebraic argument to see what value it must have.
STEP 1: Give the quantity a name.
We’ll call it \(A\) for Allistaire.
\(A = \ldots 9999\).
STEP 2: Multiply by ten
We obtain
\(10A = \ldots 99990\).
STEP 3: Subtract
We see that \(A\) and \(10A\) differ by nine (it is only their final digits that differ). Looking at \(A-10A\) we get
\(-9A=9\)
giving
\(A=-1\).
That is, our mathematics establishes that
\(\ldots 9999 = -1\).
Apparently, if we pulled out a calculator and computed the sum \(9+90+900+9000+\cdots\) the calculator will show at the end of time the answer \(-1\)!
Do you believe that?
Putting it another way: On a number line, do you believe that the numbers \(9\), \(99\), \(999\), …. are marching closer and closer to the number \(-1\)?

| Challenge: Let’s make matters worse! Consider the “number” with infinitely many \(9\)s both to the left and to the right of the decimal point: \(\ldots 9999.9999\ldots\). Use the same algebraic argument to show that this equals zero. (And this makes sense, because \(\ldots 9999.9999\ldots = \ldots 9999+ .9999\ldots = -1 + 1 = 0\).) |
It is hard to believe that \(\ldots 9999\) is a meaningful number and, moreover, it has the value \(-1\), at least in our usual way of think about arithmetic. But remember, all we proved here is that IF we choose to say that \(\ldots 9999\) is a meaningful number, then it has value \(-1\). It is up to us to decide whether or not it is meaningful quantity in the first place. Most people say it is not and stop there and that is fine.
But this begs the question:
Is there an UNUSUAL system of arithmetic for which \(\ldots 9999\) is meaningful (for which it has value \(-1\))?
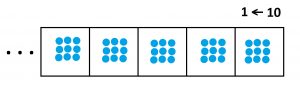
| Challenge: One might be able to argue that \(\ldots 9999\) does behave like \(-1\) in ordinary arithmetic to some degree. For example, consider performing the (very) long addition shown. Do you see the answer zero results?
If you prefer, imagine what happens if you add one dot to this loaded \(1 \leftarrow 10\) machine.
|
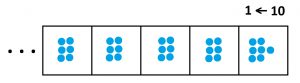
| Challenge: Try this (very) long multiplication problem. Do you see that \(\ldots 66667\) is behaving like the fraction \(\dfrac{1}{3}\)?
If you prefer, imagine what happens if you triple the count of dots in each of these boxes.
Extra: What “number” behaves like \(\dfrac{2}{3}\)? |
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()