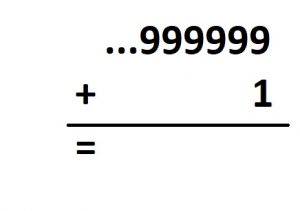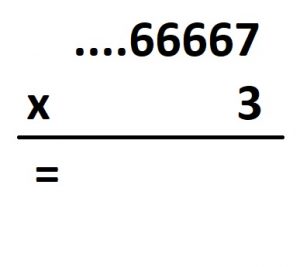Exploding Dots
10.3 Some Unusual Mathematics for Unusual Numbers
Lesson materials located below the video overview.
It is possible to develop an arithmetic system of numbers for which a quantity like \(\ldots 9999\) actually is meaningful (and by what we proved in the previous section has value \(-1\)).
Here’s one such system, one that requires we change our sense of distance between numbers on the number line. It is a system that will allow us to say, for instance, that the numbers \(9\), \(99\), \(999\), … are indeed marching closer and closer to \(-1\) on the number line despite what our geometric training says!

Warping Normal Distance on the Number Line
We usually say the number \(5\), for instance, is a distance five from \(0\) on the number line because \(5\) is five unit lengths away from the zero. (We usually use absolute value notation for this distance: \(|5|=5\).)

And \(3.7\) is a distance \(3.7\) from \(0\), \(|3.7|=3.7\), because three-and-seven-tenths of a unit fit between \(0\) and \(3.7\) on the number line. And so on.
This is a very additive way of thinking about distance: adding five \(1\)s gets you from \(0\) to \(5\); adding \(3.7\) \(1\)s get you from \(0\) to \(3.7\); and so on. We can say that the distance of a point \(a\) on the number line, in this thinking, is the number of \(1\)s that go additively into \(a\).
But much of mathematics is not only concerned with the additive properties of numbers, but also the multiplicative properties of numbers. For example, many people are interested in the prime factorizations of numbers (for example, \(1000=2^{3}5^{3}\) and \(105=3\cdot 5 \cdot 7\)). There are so many unanswered questions about the prime numbers and prime factorizations still in mathematics today. These questions are, in general, very hard!
Is there are way to bring the geometry of the number line into play to possibly help with multiplicative questions? Is there a way to think about the number line itself as perhaps structured multiplicatively rather than additively?
To think about this, rather than focus on all possible factor of numbers, let’s focus on one possible factors of numbers. And to keep matters relevant to our base-ten arithmetic thinking, let’s focus on the number \(10\).
In our additive thinking for distance on the number line we use the unit of \(1\) and ask how many ones (additively) go into each number for its distance from \(0\). We now want to use the unit of \(10\) and ask how many times ten goes multiplicatively into each number.
What could that mean?
In the world of integers the number \(0\) is the most divisible number of all: it can be divided by any integer any number of times and still give an integer result (namely \(0\)) each and every time. Focusing on our chosen factor of ten, we can divide \(0\) by ten once, or twice, or thirty-seven times, and still have an integer.
The number \(40\) is a little bit “zero-like” in this sense in that we can divide it by ten once and still have an integer. The number \(1700\) is more zero-like as it can be divided by ten twice and still give an integer result. A googol is very much more zero-like: it can be divided by ten one hundred times and still stay an integer.
The integer \(5\) is not very zero-like at all: one can’t divide it by ten even once and stay an integer.
In this setting the more times ten “goes into” into a number multiplicatively, the more zero-like it is. So in this sense, a googol is much closer to zero than \(5\) is.
So let’s develop a distance formula that regards numbers with large powers of ten as factors as closer to zero than numbers with less counts of powers of ten as factors. There are a number of ways one might think to do this, but let’s try to mimic the additive properties of the number line we are familiar with.
Normally we would say that \(850\) is further from zero than \(85\) is, and, in fact, we might even say \(850\) is ten times further from zero as \(85\) is. In our multiplicative thinking, \(850\) is now closer to zero than \(85\) is and it would be natural to have it as ten times closer.
The following formula seems a natural way to have this happen.
If \(a\) can be divided by ten a maximum of \(k\) times and remain an integer, then set \(|a|_{ten}=\dfrac{1}{10^{k}}\).
For example, then, \(|850|_{ten}=\dfrac{1}{10^{1}}=0.1\) and \(|8500|_{ten}=\dfrac{1}{10^{2}}=0.01\) and \(|8500000|_{ten}=\dfrac{1}{10^{5}}=0.00001\). Also, since \(|85|_{ten}=\dfrac{1}{10^{0}}=1\). we see, indeed, that \(850\) is ten times closer to zero than \(85\) is.
We can also measure the distance between any two numbers in this multiplicative way. For example, the distance between \(3\) and \(33\) is \(|33-3|_{ten}=|30|_{ten}=\dfrac{1}{10^{1}}=0.1\).
With this new way to measure distance, we see that
\(1\), \(10\), \(100\), \(1000\), \(\ldots\)
is a sequence of numbers getting closer and closer to zero. We have \(|1|_{ten}=1\) and \(|10|_{ten}=0.1\) and \(|100|_{ten}=0.01\) and \(|1000|_{ten}=0.001\), and so on, indeed approaching a distance of zero from \(0\).
In terms of values in a \(1 \leftarrow 10\) machine, we see that boxes far to the left in the machine, representing high powers of ten, are representing values very close to zero. (Before, in our additive thinking, boxes to the far right for decimals represented values very closer and closer to zero.)
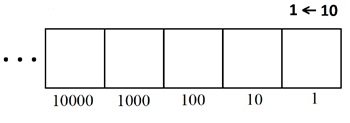
Mathematicians call this way of viewing distances between the non-negative integers ten-adic arithmetic. (The suffix adic means “a counting of operations” and here we are counting factors of ten.) It is fun to think how to extend this notion of distance to fractions too, and then to all real numbers.
The number \(\ldots 9999\)
Let’s look now at the sequence of numbers \(9\) and \(99\) and \(999\) and so on marching off to the right on the number line. Could they possibly be marching closer and closer to the value \(-1\)?

Yes, if by “closer” we mean this new multiplicative way to think of distance.
We have

The numbers \(9\), \(99\), \(999\), \(9999\), … are indeed approaching the value \(0-1=-1\).
| Comment: We can now justify the (very) long addition computation given below.
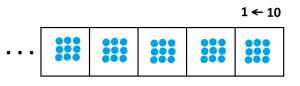
We first compute \(9+1=10\), and then we add \(90\) to this to obtain \(100\), and then we add \(900\) to obtain \(1000\), and so on. The further along we go with the computation the closer our results are to the number zero.
You can intuitively see this in the \(1 \leftarrow 10\) machine: when you add one more dot to this loaded machine and perform the explosions, one clears away dots, pushing what remains further and further to the left where boxes have less and less significant value.
Computation of this next (very) long multiplication is justified in a similar way.
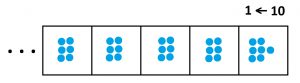
We first compute \(3 \times 7 = 21\), and then add to this \(3 \times 60\) to get \(201\), and then add to this \(3 \times 600\) to get \(2001\), and so on. Now the numbers \(20\), \(200\), \(2000\), … are getting closer and closer to zero, so the numbers \(21 = 20+1\), \(201 = 200+1\), \(2001=2000+1\), … are getting closer and closer to \(1\). The further along we go with this computation, the closer our answers are to the number \(1\). Again, we can intuitively see this reasoning at play by tripling all the values in this loaded \(1 \leftarrow 10\) machine.
And did you discover that \(\cdots |3|3|3|3|4\) behaves like the fraction \(\dfrac{2}{3}\)?
Question: Doubling \(\cdots |3|3|3|3|4\) gives \(\cdots |6|6|6|6|8\) which is one more than \(\cdots |6|6|6|6|7\), which is \(\dfrac{1}{3}\). Is this consistent? |
| Challenge: Show that in a \(2 \leftarrow 3\) machine that \(\cdots |1|1|1|1|2\) is negative one! Show that \(\cdots |0|1|0|1|0|1|0|2\) when multiplied by \(5\) gives \(1\), and so represents \(\dfrac{1}{5}\). (What measure of distance might we be using on the number line this time for these “numbers” to make sense?) |
Constructing Negative Integers
In our base-ten thinking with our multiplicative notion of distance on the number line, we set
\(|a|_{ten}=\dfrac{1}{10^{k}}\) where \(k\) is the largest count of times \(a\) can be divided by ten and remain an integer.
And we have made sense of \(\cdots 9999\) as a meaningful number with value \(-1\).
So what’s \(-2\) in this unusual system of arithmetic?
Let’s think in terms of a \(1 \leftarrow 10\) machine. Since \(-1=\cdots 9|9|9|9\) , and \(-2\) is double \(-1\), we should have
\(-2=\cdots 18|18|18|18\).
With explosions we get
\(-2=\cdots 18|18|18|18\)
\(=\cdots 18|18|19|8\)
\(=\cdots 18|19|9|8\)
\(=\cdots 19|9|9|8\)
\(=\cdots 9|9|9|8\).
And one can check that this long addition does give zero.

We can see now how to readily construct any negative integer. For example, we can see that adding \(47\) to \(\cdots 999953\) will give zero and so this latter quantity must be \(-47\), and that adding \(3000\) to \(\cdots9997000\) gives zero and so this quantity must be \(-3000\).
| Challenge: What is \(-2\) in a \(2 \leftarrow 3\) machine? What is \(-5\)? |
Constructing Fractions
We saw that \(\cdots 66667\) is the fraction \(\dfrac{1}{3}\): multiply this quantity by three and you get \(1\).
The \(1 \leftarrow 10\) machine provides a natural way to compute such fractions. For example, let’s find the ten-adic representation of \(\dfrac{4}{7}\) . That is, let’s find a number \(x\) such that \(7 \times x = 4\). Start by writing
\(x=\cdots h|g|f|e|d|c|b|a\)
as for a \(1 \leftarrow 10\) machine. Then
\(7x=\cdots 7h|7g|7f|7e|7d|7c|7b|7a\).
We want \(7a\) ,after explosions, to leave a \(4\). So we need a multiple of \(7\) four greater than a multiple of \(10\). We see that \(7a=14\) is good. So let’s set \(a=2\).
\(x=\cdots h|g|f|e|d|c|b|2\)
\(7x=\cdots 7h|7g|7f|7e|7d|7c|7b|14\)
\(=\cdots 7h|7g|7f|7e|7d|7c|7b+1|4\)
Now we want \(7b+1\) to be a multiple of \(10\) so that all dots in that box explode to leave zero behind. This suggests \(b=7\).
\(x=\cdots h|g|f|e|d|c|7|2\)
\(7x=\cdots 7h|7g|7f|7e|7d|7c|50|4\)
\(=\cdots 7h|7g|7f|7e|7d|7c+5|0|4\)
Now we need \(7c+5\) a multiple of \(10\). Choose \(c=5\).
\(x=\cdots h|g|f|e|d|5|7|2\)
\(7x=\cdots 7h|7g|7f|7e|7d|40|0|4\)
\(=\cdots 7h|7g|7f|7e|7d+4|0|0|4\)
Now choose \(d=8\).
\(x=\cdots h|g|f|e|8|5|7|2\)
\(7x=\cdots 7h|7g|7f|7e|60|0|0|4\)
\(=\cdots 7h|7g|7f|7e+6|0|0|0|4\)
And then \(e=2\).
\(x=\cdots h|g|f|2|8|5|7|2\)
\(7x=\cdots 7h|7g|7f|20|0|0|0|4\)
\(=\cdots 7h|7g|7f+2|0|0|0|0|4\)
And \(f=4\).
\(x=\cdots h|g|4|2|8|5|7|2\)
\(7x=\cdots 7h|7g|30|0|0|0|0|4\)
\(=\cdots 7h|7g+3|0|0|0|0|0|4\)
And \(g=1\).
\(x=\cdots h|1|4|2|8|5|7|2\)
\(7x=\cdots 7h|10|0|0|0|0|0|4\)
\(=\cdots 7h+1|0|0|0|0|0|0|4\)
And now I am doing the same work as I did for a value \(b\), making \(7b+1\) a multiple of \(10\). We are in a cycle and so \(x=\dfrac{4}{7}\) is represented as
\(\cdots142857 \: 142857 \: 142857 \: 2 = \overline{142857} \: 2\).
| Challenge: This process felt reminiscent of the task of writing \(\dfrac{4}{7}\) as a decimal in ordinary arithmetic using a \(1 \leftarrow 10\) machine with decimals. We argued there too that the decimal represent had to fall into a cycle.
Can you argue that the fraction \(\dfrac{2}{13}\) will also have a repeating ten-adic expansion? |
| Challenge: What is the ten-adic expansion of \(-\dfrac{4}{7}\) ?
One approach: Write \(-\dfrac{4}{7}\) as \(\overline{-1|-4|-2|-8|-5|-7} \:|- 2\) and add some dots and antidot pairs to make all the terms positive.
\(\overline{-1|-4|-2|-8|-5|-7} \:|- 2\) \(=\overline{-1|-4|-2|-8|-5|-7} \:|- 2+\left(-8+8\right)\) \(=\overline{-1|-4|-2|-8|-5|-7-1} \:|8\) \(=\cdots\) |
A Glitch
Let’s try to compute the ten-adic representation of the fraction \(\dfrac{1}{2}\). Here we seek a number
\(x=\cdots h|g|f|e|d|c|b|a\)
so that
\(2x=\cdots 2h|2g|2f|2e|2d|2c|2b|2a\)
equals \(1\).
This means we a number \(a\) so that, after explosions, \(2a\) leaves a single dot. That is, we need \(2a\) to be one more than a multiple of ten. This is not possible!
| Challenge: Contemplate the ten-adic expansions for \(\dfrac{1}{5}\) and \(\dfrac{3}{10}\) and \(\dfrac{2}{35}\).
In general, which fractions \(\dfrac{p}{q}\) seem to be problematic? |
| Challenge: Develop a general theory that if \(\dfrac{p}{q}\) is a reduced fraction with \(q\) sharing no factor in common with ten (other than \(1\)), then it is for certain possible to express \(\dfrac{p}{q}\) as a ten-adic number \(\cdots hgfedcba\). Show further that its expression is sure to fall into a repeating cycle. |
Broadening our Definition a Tad
It seems we have defined a ten-adic value to be an expression of the form \(\cdots edcba\) with each digit one of the standard digits \(0\) through \(9\), allowing for non-zero digits to appear infinitely far to the left.
In this system we have the ordinary positive integers,
eg \(5\) is \(\cdots 00005\),
the negative numbers
eg \(-5\) is \(\cdots 99995\)
and some fractions
eg \(\dfrac{1}{3}\) is \(\cdots 66667\).
But not all fractions. It turns out that the troublesome fractions are the ones \(\dfrac{p}{q}\) which, when written in reduced form, have a denominator a multiple of \(2\) or \(5\) or both.
We can obviate this problem if we allow a ten-adic number to extend finitely far into the decimal places on the right. That is, set a ten-adic expression to be one of the form \(\cdots edcba.xy\ldots z\) with each digit one of the standard digits \(0\) through \(9\), allowing for non-zero digits to appear infinitely far to the left of the decimal point, and only finitely far to its right. (After all, we do the analogous thing in ordinary arithmetic by writing \(33.3333\cdots\), for example, for thirty-three and a third.)
Now we have
\(\dfrac{1}{2}=0.5\) is \(\cdots 0000.5\)
and
\(\dfrac{23}{100}=0.23\) is \(\cdots 0000.23\).
We can also handle \(\dfrac{2}{35}\) by thinking of this as \(\dfrac{2}{7 \times 5}=\dfrac{2\times 2}{7 \times 10}=\dfrac{4/7}{10}\). Since \(\dfrac{4}{7}\) is \(\overline{142857} \: 2\) we must have \(\dfrac{2}{35}=\overline{142857}.2\).
| Challenge: Show that \(\dfrac{1}{6}=\cdots 3333.5\) and hence find the ten-adic expression for \(\dfrac{5}{12}=\dfrac{1}{6}+\dfrac{1}{4}\).
What is the ten-adic expression for \(\dfrac{1}{12}\)? |
| Challenge: Explain why every fraction is now sure to have a ten-adic representation. |
| Challenge: Show that \(\overline{53}23=\cdots53535323\) is the number \(-\dfrac{1000}{33}\) in ten-adic arithmetic. (Hint: Multiply the quantity by \(100\) and subtract.)
One can use the technique of this question to show that every ten-adic number that eventually falls into a cycle going leftwards is a rational number. |
| Challenge: In ordinary arithmetic, the quantity \(0.abcabcabc\cdots=0.\overline{abc}\) is the fraction \(\dfrac{abc}{999}\). We see this by setting \(x=0.abcabcabc\cdots\) and noticing that \(1000x=abc.abcabcabc\cdots\). Subtracting then yields \(999x=abc\).
Show that the same algebra applied to the ten-adic number \(\cdots abcabcabc=\overline{abc}\) shows that it this number has value \(-\dfrac{abc}{999}\).
In fact, prove the following general result. Suppose \(b_{1}\), \(b_{2}\), …, \(b_{k}\) are single digits.
If \(0.\overline{b_{1} b_{2}\ldots b_{k}}\) is the fraction \(\dfrac{p}{q}\) in ordinary arithmetic, then \(\overline{b_{1} b_{2} \ldots b_{k}}\) is the fraction \(-\dfrac{p}{q}\) in ten-adic arithmetic, and vice versa. |
| Challenge: Explore a theory of “3/2-adic” representations of fractions using a \(2 \leftarrow 3\) machine. |
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()