With the ten-adic numbers we can represent all integers and fractions. But did you notice that all the numbers we presented so far have repeating cycles?

We can also consider numbers in this system, with infinitely many digits to the left, that don’t fall into repeating cycles. These must correspond to irrational numbers. (And possibly other new types of numbers?)

We can add and multiply ten-adic numbers. For example, we have seen \(\cdots 66667\) is \(\dfrac{1}{3}\) and \(\cdots 9999\)  is \(-1\).  We can compute their sum to see an answer indeed one less than \(\cdots 6667\). (And \(\cdots 6666\)  is \(-\dfrac{6}{9} = -\dfrac{2}{3} = \dfrac{1}{3}-1\).)

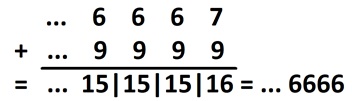
And we can compute their product to see the answer \(\cdots 3333\), which is indeed \(-\dfrac{1}{3}\).

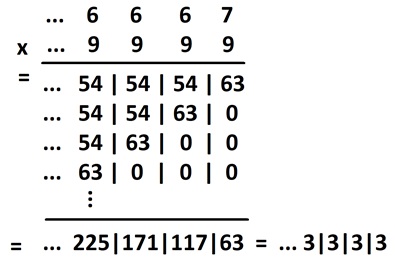
And since we know how to make negative ten-adic numbers and fractions as ten-adic numbers, we can also subtract (add the negative) and divide (multiply by a fraction) ten-adic numbers.

Well, almost. We can’t divide by some ten-adic numbers. There’s a flaw in the ten-adic system.

Here’s an example of the problem. We have that

\(2 \times 5=10\) is a number close to zero.

\(2^{2} \times 5^{2}=100\) is a number closer to zero.

\(2^{3} \times 5^{3}=1000\) is a number even closer to zero.

And so on.

It is possible to construct a non-zero ten-adic number \(N\) that behaves like an infinitely large power of two and a non-zero ten-adic number \(M\) that behaves like an infinitely large power of five, so their product then, \(N \times M\), is so close to zero that it actually is zero!

\(N \times M = 0\)

Non-zero numbers that multiply to zero don’t exist ordinary arithmetic, but they do in the ten-adic system. This means we can’t divide by some non-zero numbers, like \(N\) and \(M\) in this arithmetic. (If dividing by \(N\) is possible, then divide the equation  \(N \times M = 0\) through by \(N\) and get the contradictory statement that \(M=0\).)

How might one construct these numbers \(N\) and \(M\)? It’s a bit tricky, but here’s the gist of it.

Here are the first few powers of five:

\(5\), \(25\), \(125\), \(625\), \(3125\), \(15625\), \(78125\), …

All of these powers end in \(5\).

Infinitely of them actually end in \(25\).

Actually, one can verify that infinitely of then actually end in \(125\). (Multiply any one that does by \(25\) to get another one.)

Actually, infinitely many of them end in \(3125\). (Multiply any on that does by \(625\) to find another one that does.)

And so on.

In principle, we can construct a ten-adic number \(M=\cdots 3125\) for which there are infinitely many powers of five that end with the same set of digits as \(M\) does, for any size set of digits you want. (There are infinitely many powers of five that end with the final set of one-hundred digits as \(M\) does, and there are infinitely many powers of five that end with the same million final digits, and so on.)

We can do the same construction for the powers of two and construct a ten-adic number \(N=\cdots 832\) for which there exist infinitely many powers of two that end with any final set of digits of \(N\).

Now look what happens when you multiply \(N\) and \(M\). You do indeed get zero.

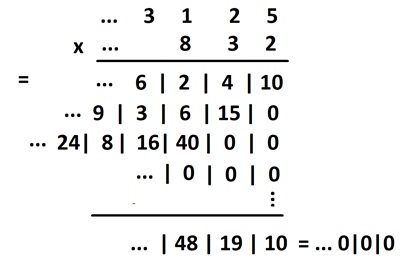
The problem is that \(10\) is a composite number. One can prove that this annoyance will never arise if one works in base that is a prime number instead!

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources