The concept of Exploding Dots has been around for many centuries, though not necessarily visualized as dots in boxes (and certainly not as exploding dots).

The ancient counting and arithmetic device, an abacus, is simply a \(1 \leftarrow 10\) machine. Its simplest version is just a series of rods held in a frame with each rod holding ten beads. One slides beads up rods to represent numbers and, in performing calculations, whenever ten beads reach the top of one rod, one slides them down (they “explode”) and raises one bead up on the rod one place to their left in their stead.

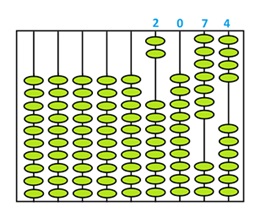
Comment: A more modern abacus has a cross bar with five beads on each rod below the bar and two beads above it, with each of those two beads representing a group of five. One slides beads to touch the cross bar. Thus “8,” for example, is represented on a rod as three beads touching the cross bar from below and one bead touching the cross bar from above. This version of the abacus is a \(1 \leftarrow 10\) machine that has a special dot (a blue dot, perhaps) that represents five dots in a box.

Five centuries ago, Scottish mathematician John Napier (1550 – 1617),  best known for his invention of logarithms, actually discovered and worked with a \(1 \leftarrow 2\) machine,  but he found it useful to stack rows of boxes on top of one another to make a grid of squares, with each row being its own \(1 \leftarrow 2\) machine.

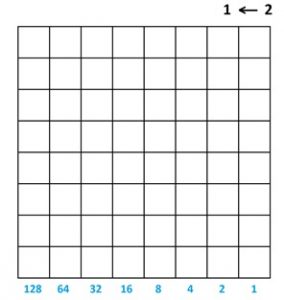
He suggested using a physical copy this grid, a wooden board or square sheet of cloth marked into squares, and beads or counters.

With this board, Napier showed the world how to add, subtract, multiply and divide numbers. He also felt it was useful for computing integer square roots of numbers!

Read on to see how. (The next few lessons have videos that explain how to use Napier’s checkerboard abacus too.)

References:  Martin Gardner wrote about this work in his article “Napier’s Chessboard Abacus” which appears as chapter 8 in Knotted Doughnuts and Other Mathematical Entertainments (W.H.Freeman and Company, 1986) but not in terms of  machines. Also S. Kolpas and E. Tomash have recently produced a lovely series of pieces on this topic: Napier’s Binary Chessboard Calculator. See the MAA website here.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources