This is where Napier’s brilliance starts to shine.

Napier suggested not only labeling each column with a power two, but to also label each row this way too.  A dot in any box is then given the value of the product of its column and row numbers. For example, one dot in this picture has value \(64 \times 32\ = 2048\) and the other has value \(4 \times 4 = 16\), and together they represent the number \(2048+16=2064\).  One can thus represent very big numbers on this two-dimensional array.

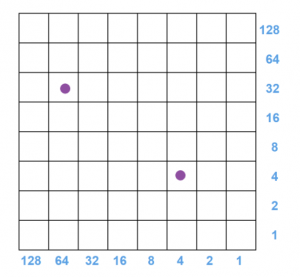
Moreover, not only does each row operate as its own \( 1 \leftarrow 2\) machine, each column now does too!

Any two dots in a cell can be erased—they explode, “kaboom”—and be replaced by one dot either one cell to their left or by one dot one cell above them, your choice!

One can also unexplode dots.

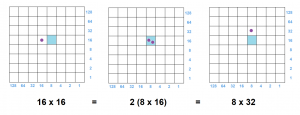
Question: Explain why dots in the light blue cells will have the same value. Explain why dots in the light purple cells will have the same value.

Napier noted too that you can slide a dot anywhere on the southwest diagonal on which it sits and not change its value and hence not the total value of several dots on in the grid either.

By placing dots in the grid we can represent large numbers, and by performing slides, explosions, and unexplosions we can change the representations of those numbers in lots of different—but always equivalent—ways. And with this power, Napier realized we can perform some sophisticated arithmetic!

Question: The dots in each each of these two boards have total value 80. (Check this!)

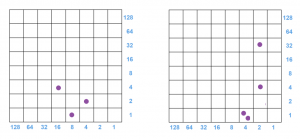 Can you perform some slides and/or explosions and/or unexplosions to convert the picture of dots on the left to the picture of dots on the right?

Can you continue changing the positions of dots with legitimate moves to create a representation of the number with dots only in the rightmost column, at most one dot per cell?  How about with all dots on the bottom row with at most one dot per cell?

Multiplication

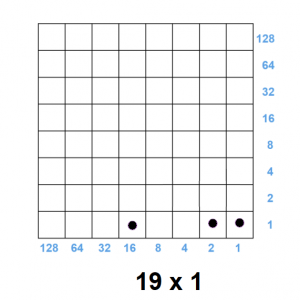
The number \(19\) has \(1 \leftarrow 2\) code \(10011\). We can display this number in the bottom row of the checkerboard as \( 16 \times 1 + 2 \times 1 + 1 \times 1\). (Since the bottom row of the checkerboard is its own \(1 \leftarrow 2\) machine, one could place \(19\) dots into the right corner box and perform explosions in just the bottom row to get this binary code.)

Here’s a picture of one copy of \(19\) plus four copies of \(19\), that is, here is a picture of \(19 \times 5\).

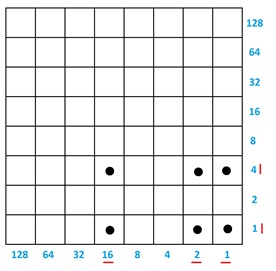
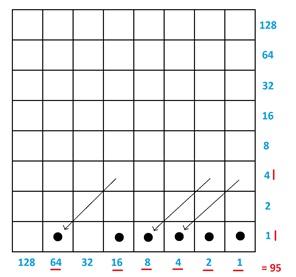
Slide each dot diagonally downward to the bottom row: this does not change the total value of the dots in the picture. The answer \(95\) appears. We’ve just conducted a multiplication computation!

More complicated multiplication problems will likely require using a larger grid and performing some explosions. For example, here is a picture of \(51 \times 42\). (We see \(51\) as  \(32 + 16 +2+1\) and we have \(2\) copies of this plus \(4\) copies of this plus \(32\) copies of this.)

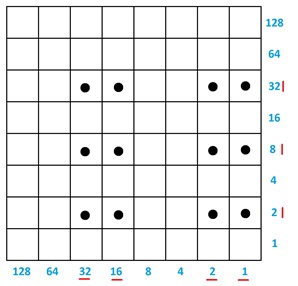
Sliding gives this picture

and the bottom row explodes to reveal the answer \(2142\).

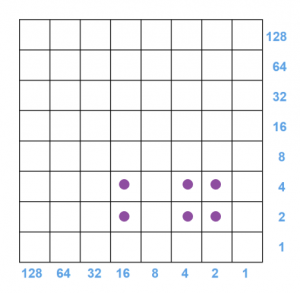
Question:  a) What product is represented in this checkerboard? What is the answer to the product?

b) Compute \( 8 \times 8\) and  \(10 \times 10\) and \(15 \times 15\) with a checkerboard.

c) Compute \(37 \times 18\) with a checkerboard.

d) Keep computing different products via Napier’s method. Have some fun!

Question: Let’s do the multiplication backwards! Let’s see if we can compute \(108 \div 9\) and \(65 \div 5\) on the checkerboard. 

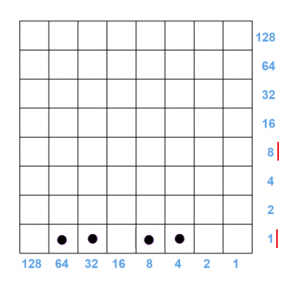
a) Here’s the result of multiplying some number by \(9\) with Napier’s checkerboard. What number was multiplied by \(9\)? Can you see the answer by sliding dots to recreate the original multiplication problem?

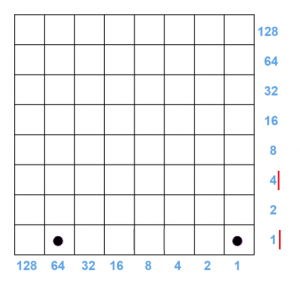
b) The result of multiplying some number by is \(5\) as \(65\) shown. Can you recreate the original multiplication problem by unexploding and sliding dots?

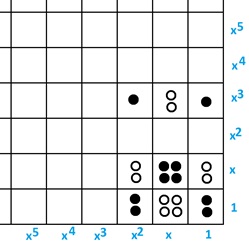
Question:  One can do polynomial multiplication with the checkerboard too! (One needs two different colored counters: one for dots and one for antidots.) Do you see how this picture represents \(\left(x^{2}-2x+1\right)\left(x^{3}-2x+2\right)\)? Do you see how to get the answer \(x^{5}-2x^{4}-x^{3}+6x^{2}-6x+2\) from it?

Question:  How would you display the product \(\left(1-x\right) \left(1+x+x^2+x^3+x^4+\cdots\right)\)? What answer does it give?

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources