Here is a video, in Spanish, from the team of Goldfish & Robin and Friends, “kids explain math to kids”  going through the details of the 1<–3 machine. And here is a video in English on some more about the 1<–3 machine.

We’re now set to think our way through the meaning of all sorts of machines. (See the video in the previous lesson.)

As usual, my solutions to these questions appear in the final section of this chapter.

4. In a $1 \leftarrow 3$ machine, three dots in any one box are equivalent to one dot one place to the left. (And each dot in the rightmost box is again worth $1$.)  We get the dot values in this machine by noting that three $1$s is $3$, and three $3$s is $9$, and three $9$s is $27$, and so on.

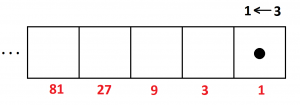
a) What is the value of a dot in the next box to the left after this?

At one point we said that the $1 \leftarrow 3$ code for fifteen is $120$. And we see that this is correct: one $9$ and two $3$s does indeed make fifteen.

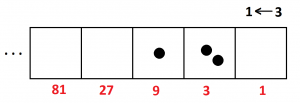
b) Could we say that the$1 \leftarrow 3$ code for fifteen is $0120$?  That is, is it okay to put zeros in the front of these codes? What about zeros at the ends of codes? Are they optional? Is it okay to leave off the last zero of the code $120$ for fifteen and just write instead $12$?

c) What number has $1 \leftarrow 3$ machine code $21002$?

d) What is the $1 \leftarrow 3$ machine code for two hundred?

The $1 \leftarrow 3$  machine codes for numbers are called ternary or base three representations of numbers. Only the three symbols $0$, $1$, and $2$ are ever needed to represent numbers in this system.

There is talk of building optic computers based on polarized light: either light travels in one plane, or in a perpendicular plane, or there is no light. For these computers, base-three arithmetic would be the appropriate notational system to use.

 5. In the $1 \leftarrow 4$ system four dots in any one box are equivalent to one dot one place to their left. What is the value of a dot in each box?

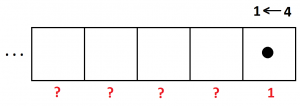
b) What is the $1 \leftarrow 4$  machine code for twenty nine?

c) What number has $132$ as its $1 \leftarrow 4$ machine code?

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources