As promised, here are my solutions to the questions posed.

1. Here are the values of a single dot in each of a few more boxes.

Care to keep going?

2. Thirty-seven.

3. \(11001000\)

4. a)  Each dot in the next box to the left is worth three \(81\)s, that’s \(243\).

b) Yes it is okay to insert a zero at the front of the code. This would say that there are no \(27\)s, which is absolutely correct. Deleting the end zero at the right, however, is problematic. \(120\) is the code for fifteen (one \(9\)and two \(3\)s) but \(12\) is the code for five (one \(3\) and two \(1\)s).

c) One hundred and ninety one. (Two \(81\)s, one \(27\), and two \(1\)s.)

d) \(21102\)

5. a) For a \(1 \leftarrow 4\) machine, boxes have the following values:

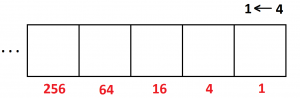
b) The number twenty-nine has code \(131\) in a \(1 \leftarrow 4\).

c) Thirty. (This is one more than the code for twenty-nine!)

6. Might Martians use base twelve? This means they will need twelve different symbols for writing numbers.

By the way, have you noticed that we use ten different symbols  –  \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\), and \(0\)- which we call digits. (We call our fingers digits too!)

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources