How does this dots-and-boxes approach to addition compare to the standard algorithm most people know?

Let’s go back to the example \(358+287\). Most people are surprised (maybe even perturbed) by the straightforward left-to-right answer \(5|13|15\).

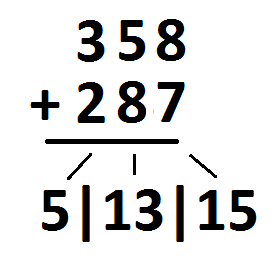
This is because the traditional algorithm has us work from right to left, looking at \(8+7\) first.

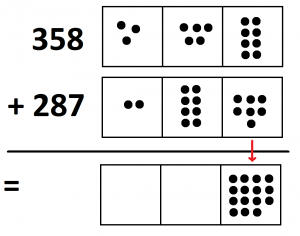
But in the algorithm we don’t write down the answer \(15\). Instead, we explode ten dots right away and write on paper a \(5\) in the answer line together with a small \(1\) tacked on to the middle column. People call this carrying the one and it – correctly – corresponds to adding an extra dot in the tens position.

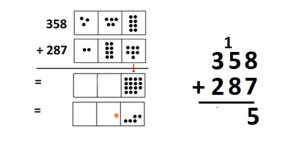
Now we attend to the middle boxes. Adding gives \(14\) dots in the tens box (\(5+8\) gives thirteen dots, plus the extra dot from the previous explosion).

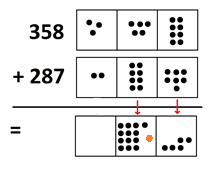
And we perform another explosion.

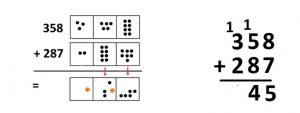
On paper, one writes “\(4\)” in the tens position of the answer line, with another little “\(1\)” placed in the next column over. This matches the idea of the dots-and-boxes picture precisely.

And now we finish the problem by adding the dots in the hundreds position.

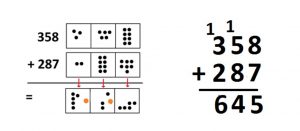
So the traditional algorithm works right to left and does explosions (“carries”) as one goes along. On paper it is swift and compact and this might be why it has been the favored way of doing long addition for centuries.

The Exploding Dots approach works left to right, just as we are taught to read in English, and leaves all the explosions to the end. It is easy to understand and kind of fun.

Both approaches, of course, are good and correct. It is just a matter of taste and personal style which one you choose to do. (And feel free to come up with your own new, and correct, approach too!)

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources