Let’s keep playing with the \(1 \leftarrow 10\) machine. And let’s do a multiplication problem … right now!

You’ve got less than three seconds to write down an absolutely correct speedy answer to this multiplication problem. What’s a good answer?

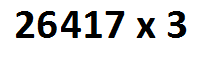
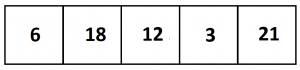
Can you see that \(6|18|12|3|21\), that is, “six ten thousand, eighteen thousand, twelve hundred and threety twenty-one,” is correct and does the speedy trick?

Here’s what’s going on.

Let’s start with a picture of 26417 in a \(1 \leftarrow 10\) machine. (Is it okay if I just write numbers rather than draw dots?)

We’re being asked to triple this number.             

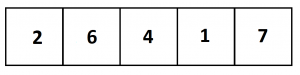
Right now we have \(2\) ten-thousands. If we triple this, we’d have \(6\) ten-thousands.

Right now we have \(6\) thousands, and tripling would make this \(18\) thousands.

Also, \(4\)  hundreds becomes  \(12\) hundreds; \(1\)  ten becomes \(3\) tens; and \(7\) ones becomes \(21\) ones.

\(6|18|12|3|21 = 6|19|2|3|21 = 6|19|2|5|1  = 7|9|2|5|1\)

The answer \(79251\) appears.

2. Compute each of the following: \(26417 \times 4\), \(26417 \times 5\), and \(26417 \times 9\).

Compute \(26417 \times 10\)and explain why the answer has to be \(264170\). (This answer looks like the original number with the digit zero tacked on to its end.)

Extra: Care to compute \(26417 \times 11\) and \(26417 \times 12\) too? (The answer could be “No! I do not care to do this!”)

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources