Check out Goldfish & Robin’s “Where Young Minds Collide” videos taking the ideas of this lesson further: Multiplicaton in a 1 <–2 Machine ;  Multiplication in 1 <– 3 Machine ;  More than just Multiplication in a 1 <– 2 Machine. 

And here is yet another way to think about multiplication, by linking it to the distributive property.  

Is it possible to do, say, \(37 \times 23\), with dots and boxes?

Here we are being asked to multiply three tens by \(23\) and seven ones by \(23\). If you are good with your multiples of \(23\), this must give \(3 \times 23 = 69\) tens and \(7 \times 23 = 161\) ones.  The answer is thus \(69|161\). With explosions this becomes \(851\).

But this approach seems hard! It requires you to know multiples of \(23\).

Thinking Exercise:

Suzzy thought about \(37 \times 23\) for a little while, she eventually drew the following diagram.

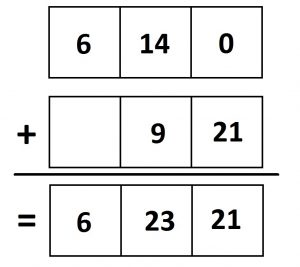
She then said that \(37 \times 23 = 6|23|21=8|3|21=851\).

a) Can you work out what Suzzy was thinking? Here’s another example she later did.

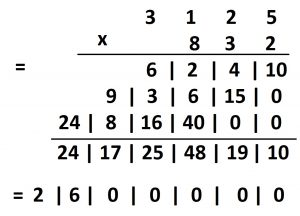
b) What diagram do you think Suzzy might draw for \(236 \times 34\) (and what answer will she get from it)? 

c) Using Suzzy’s approach do \(37 \times 23\) and \(23 \times 37\) give the same answer? Is it obvious as you go through the process that they will? Do \(236 \times 34\)  and \(34 \times 236\)  give the same answer in Suzzy’s approach?

Here’s another fun way to think about multiplication. Let’s work with a \(1 \leftarrow 2\) machine this time.

Let’s compute \(13 \times 3\).

Here’s what \(13\) looks like in a \(1 \leftarrow 2\) machine.

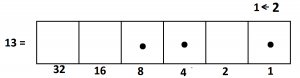
We’re being asked to triple everything. So each dot we see is to be replaced with three dots.

And now we can do some explosions to see the answer  \(39\) appear (which is \(100111\) in the \(1 \leftarrow 2\) machine).

Alternatively, we can notice that three dots in a \(1 \leftarrow 2\) machine actually look like this.

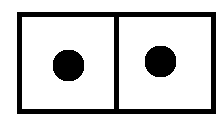
So we can replace each dot in our picture of \(13\) instead by one dot and a second dot one place to the left. (I’ve added some color to the picture to help.)

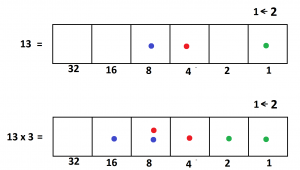
Now with less explosions to do, we see the answer \(100111\) appear.

We can follow this latter approach in base ten too, if we like, but it is likely to be unpleasant and messy! (I personally like Suzzy’s approach in the Thinking Exercise above.)

Let’s consider \(37 \times 23\) again. Here’s what \(37\) looks like.

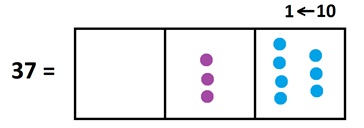
To multiply by \(23\) we need to replace each single dot with twenty-three dots. But \(23\) looks like two-dots-next-to-three dots in a \(1 \leftarrow 10\) machine, we can replace each dot with two dots and three dots.

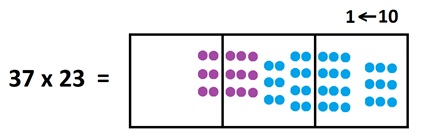
We see the answer \(6|21|23\), which explodes to give the answer \(851\).

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources