In the last section we saw that \(276 \div 12\) equals \(23\).

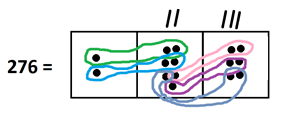
Suppose we tried to compute \(277 \div 12\) instead. What picture would we get? How should we interpret the picture?

Well, we’d see the same picture as before except for the appearance of one extra dot, which we fail to include in a group of twelve.

This shows that \(277 \div 12\) equals \(23\) with a remainder of \(1\).

You might write this as

\(277 \div 12  = 23 R1\)

or with some equivalent notation for remainders. (People use different notations for remainders in different countries.) Or you might be a bit more mathematically precise and say that \(276 \div 12\) equals \(23\) with one more dot still to be divided by twelve:

\(277 \div 12 = 23 + \dfrac{1}{12}.\)

Here are some questions to try, if you want.

9. Compute \(2789 \div 11\).

10. Compute \(4366 \div 14\).

11. Compute \(5481 \div 131\).

As you play with division in dots-and-boxes you might decide that it is actually good to always work from left to right in case there are remainders: we’d like all the “extra” dots we see appear in the lower places, the ones and tens places, rather than the higher thousands places, for instance. (But even if you don’t choose to do this, you won’t go wrong! Unexplosions will always be possible to help you out.)

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources