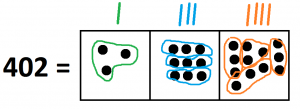
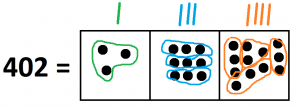
Here’s the dots and boxes way to show that \(402 \div 3\) equals \(134\).

This looks nothing like the approach one is usually taught in schools to solve division problems. For example, many schools have students compute \(402 \div 3\) with an algorithm that looks something like this.

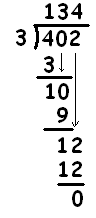
At first glance this seems very mysterious, but it is really no different from the dots and boxes method. To see why, let’s first explore an estimation method for division also often taught to students. It goes as follows:

To compute \(402 \div 3\) we need to figure out the number of groups of three we can find in \(402\).

Let’s first make a big guess, say, one hundred groups of three.

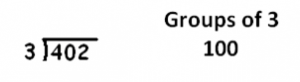
How much is left over after taking away one hundred groups of three? Answer: \(102\).

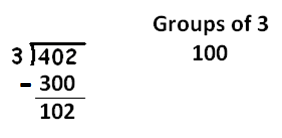
How many groups of three are there in this remaining \(102\)? Let’s guess \(30\).

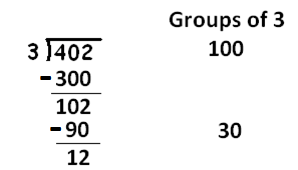
That leaves twelve. And there are four groups of three in twelve.

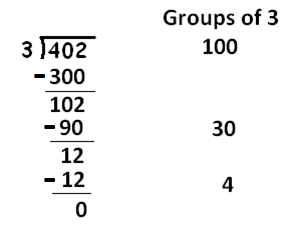
This accounts for the entire count of \(402\). We see that there are \(134\) groups of three in this count.

The dots and boxes method is doing exactly the same work, but purely visually.

And the table we first presented is also identical to this estimation method. It was invented just to use less ink as it doesn’t write down quite as much. (It skips rewriting some digits.)

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

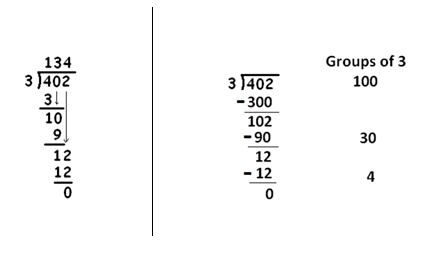
Resources