As promised, here are my solutions to the question posed.

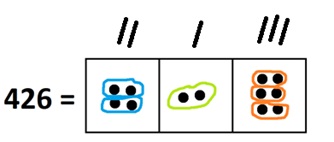
1. We see two groups of two at the hundreds level, one group of two at the tens level, and three orange groups of two at the ones level. Thus \(402\) is a picture of \(213\) that got doubled. So \(426 \div 2 = 213\).

2. Here’s a picture of \(402\).

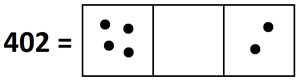
We’re looking for groups of three in it. We see one group at the hundreds level.

Now we seem to be stuck. But an unexplosion gets us moving again!

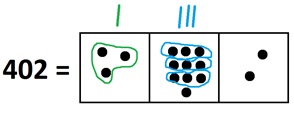
And another unexplosion.

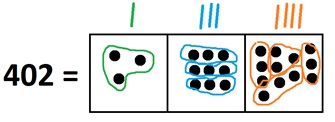
Now we see that there are one hundred, three tens, and four groups of three in the quantity \(402\). Thus \(402 \div 3 = 134\).

3. In the picture for \(404 \div 3\) we see two leftover dots unaccounted for.

So \(404 \div 3\) equals \(134\) with a remainder of \(2\).

Note: We could regard this remainder as “two dots still to be divided by three,” and so write

\(404 \div 3 = 134 +\dfrac{2}{3}\).

4. We certainly see one group of five right away.

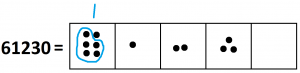
Let’s perform some unexplosions. (And let’s write numbers rather than draw lots of dots. Drawing dots gets tedious!)

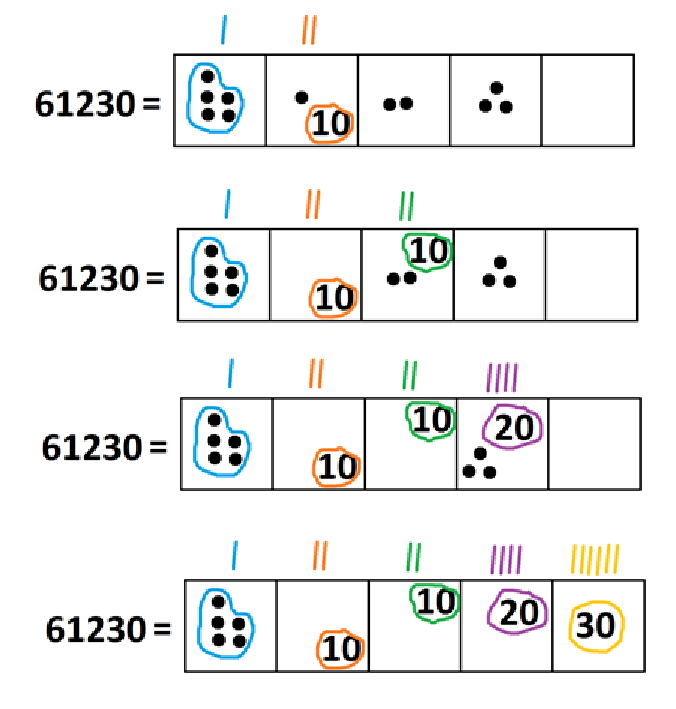
We see \(61230 \div 5 = 12246\).

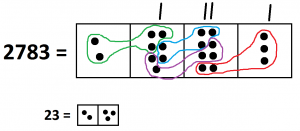
5. \(2783 \div 23 = 121\).

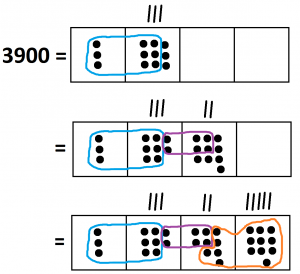
6. \(3900 \div 12 = 325\).We need some unexplosions along the way. (And can you see how I am getting efficient with my loop drawing?)

7. \(46632 \div 201 = 232\).

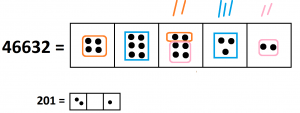
8. 

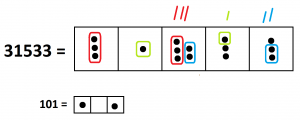
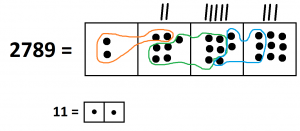
9. We have \(2789 \div 11 = 253\) with a remainder of \(6\). That is, \(2789 \div 11 = 253 + \dfrac{6}{11}\).

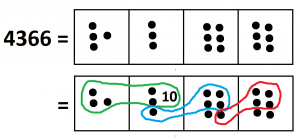
10. \(4366 \div 14 = 311 +\dfrac{12}{14}\).

11. \(5481 \div 131 = 41 +\dfrac{110}{131}\).

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources