Check out Goldfish & Robin and Friend’s “Where Young Minds Collide” video on this topic: Kids Explain Math For Kids.

 

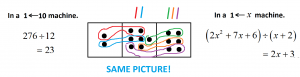
Here’s the division problem \(276 \div 12\) we did earlier in a \(1 \leftarrow 10\) machine. We see the answer \(23\). Stare at this picture for a moment – it will soon sneak back up on us.

 

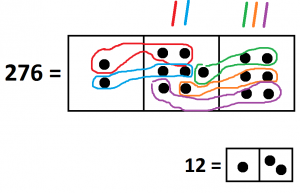
Let’s now do the same division problem in another base. But the only tricky part is that I am not going to tell you which machine we are in! We could be in a \(1 \leftarrow 10\) machine again, I am just not going to say. Maybe it will be in a \(1 \leftarrow 2\) machine, or a  \(1 \leftarrow 4\) machine or a \(1 \leftarrow 13\) machine. You just won’t know as I am not telling. It’s the mood I am in!

 

Now, in high school algebra there seems to be a favorite letter of the alphabet to use for a quantity whose value you do not know. It’s the letter \(x\).

 

So let’s work with an \(1 \leftarrow x\) machine with the letter \(x\) representing some number whose actual value we do not know.

 

In a \(1 \leftarrow 10\) machine the place values of the boxes are the powers of ten: \(1\), \(10\), \(100\), \(1000\), … .

In a \(1 \leftarrow 2\) machine the place values of the boxes are the powers of two: \(1\), \(2\), \(4\), \(8\), \(16\), ….

And so on.

Thus, in an \(1 \leftarrow x\) machine, the place values of the boxes will be the powers of \(x\).

 

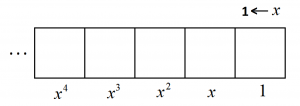
As a check, if I do tell you that \(x\) actually is \(10\) in my mind, then the powers \(1\), \(x\), \(x^{2}\), \(x^{3}\), … match the numbers \(1\), \(10\), \(100\), \(1000\), … , which is correct for a \(1 \leftarrow 10\) machine. If, instead, I tell you \(x\) is really \(2\) in my mind, then the powers \(1\), \(x\), \(x^{2}\), \(x^{3}\), … match the numbers \(1\), \(2\), \(4\), \(8\), \(16\), …, which is correct for a \(1 \leftarrow 2\) machine.

This \(1 \leftarrow x\) machine really is representing all machines all at once!

 

Okay. Out of the blue! Here’s an advanced high school algebra problem.

 

Compute \(\left(2x^2+7x+6\right)\div\left(x+2\right)\).

 

Can you figure out what this means on an \(1 \leftarrow x\)  machine? Try playing with this before reading on.

 

 

Here’s what \(\left(2x^2+7x+6\right)\) looks like in an \(1 \leftarrow x\) machine. It’s two \(x^2\)s, seven \(x\)s, and six ones.

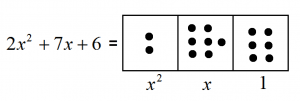
And here’s what \(x+2\) looks like.

The division problem \(\left(2x^2+7x+6\right)\div\left(x+2\right)\) is asking us to find copies of \(x+2\) in the picture of \(2x^2+7x+6\).

 

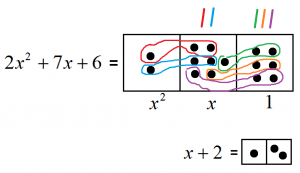
I see two copies of \(x+2\) at the \(x\) level and three copies at the \(1\) level. The answer is \(2x+3\).

(The picture is showing us how to view \(2x^2+7x+6\) as \((x+2)\times x + (x+2)\times x + (x+2)\times 1 + (x+2)\times 1 + (x+2)\times 1\) . Nifty!)

 

Stare at the picture for \(\left(2x^2+7x+6\right)\div\left(x+2\right)=2x+3\). Does it look familiar?

 

We’ve just done a high school algebra problem as though it is a grade school arithmetic problem!

 

What’s going on?

 

Suppose I told you that \(x\) really was \(10\) in my head all along. Then \(2x^2+7x+6\) is the number \(2\times 100 + 7\times 10 +6\), which is \(276\). And \(x+2\) is the number \(10+2\), that is, \(12\). And so we computed \(276 \div 12\). We got the answer \(2x+3\), which is \(2\times10 +3=23\), if I am indeed now telling you that \(x\) is \(10\).

In fact, when we computed \(276 \div 12\), we circled two groups of twelve, \(10+2\), at the tens level and three groups of \(10+2\) at the ones level, just as the polynomial division problem does with \(x+2\).

So we did just repeat a grade-school arithmetic problem!

 

Aside: By the way, if I tell you that \(x\) was instead \(2\), then

\(2x^2+7x+6\) equals \(2\times4+ 7\times 2 +6\), which is \(28\),

\(x+2\) equals \(2+2\), which is \(4\),

and

\(2x+3\) equals \(2\times2+3\), which is \(7\).

We just computed \(28 \div 4 = 7\), which is correct!

Doing division in an \(1 \leftarrow x\) machine is really doing an infinite number of division problems all in one hit. Whoa!

 

Try computing \(\left(2x^{3}+5x^2+5x+6\right)\div \left(x+2\right)\) in an \(1 \leftarrow x\) machine to get the answer \(2x^2+x+3\). (And if I tell you \(x\) is \(10\) in my mind, can you see that this matches \(2556 \div 12 = 213\)?)

 

 

In high school, numbers expressed in an \(1 \leftarrow x\) machine are usually called polynomials. They are just like numbers expressed in base \(10\), except now they are “numbers” expressed in base \(x\). (And if someone tells you \(x\) is actually \(10\), then they really are base-ten  numbers!)

 

Keeping this in mind makes so much of high school algebra so straightforward: it is a repeat of grade school base-ten arithmetic.

 

 

Here are some practice problems for you to try, it you like. My answers to them appear in the final section of this chapter.

 

1. a) Compute \(\left(2x^{4}+3x^{3}+5x^{2}+4x+1\right)\div\left(2x+1\right)\).

     b) Compute \(\left(x^{4}+3x^{3}+6x^{2}+5x+3\right)\div\left(x^2+x+1\right)\).

If I tell you \(x\) is actually \(10\) in both these problems what two division problems in ordinary arithmetic have you just computed?

 

2. Here’s a polynomial division problem written in fraction notation. Can you do it? (Is there a slight difficulty to watch out for?)

\(\dfrac{x^{4}+2x^{3}+4x^{2}+6x+3}{x^2+3}\)

 

 

3. Show that \(\left(x^{4}+4x^{3}+6x^{2}+4x+1\right)\div\left(x+1\right)\) equals \(x^{3}+3x^{2}+3x+1\).

a) What is this saying for \(x=10\)?

b) What is this saying for \(x=2\)?

c) What is this saying for \(x\) equal to each of 3, 4, 5, 6, 7, 8, 9, and 11?

d) What is it saying for \(x=0\)?

e) What is it saying for \(x=-1\)?

 

Factoring

Sometimes you might be lucky and see in a picture common groups. For example, in this picture of \(x^2 + 5x + 6\) can you see some common groups?

Maybe you see this?

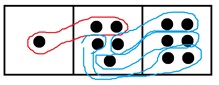
This shows that \(x^2 + 5x + 6 = \left(x+2\right) \left(x+3\right)\). Maybe you saw common groups of \(x+3\) first, instead! (What loops do you draw to see them?)

Resources