See how Goldfish & Robin multiply polynomials in this video where kids explain math to kids.

Can we multiply polynomials? You bet!

Here’s the polynomial \(2x^2-x+1\).

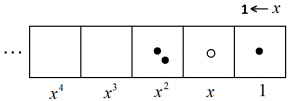
If we want to multiply this polynomial by \(3\) we just have to replace each dot and each antidot with three copies of it. (We want to triple all the quantities we see.)

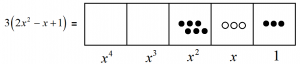
We literally see that \(3\left(2x^2-x+1\right)\) is \(6x^2-3x+3\).

Suppose we wish to multiply \(2x^2-x+1\) by \(-3\) instead. This means we want the anti-version of tripling all the quantities we see. So each dot in the picture of \(2x^2-x+1\) is to be replaced with three antidots and each antidot with three dots.

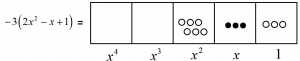
We have \(-3\left(2x^2-x+1\right)=-6x^2+3x-3\). We could also say that \(-3\left(2x^2-x+1\right)\) is the anti-version of \(3\left(2x^2-x+1\right)\).

Now suppose we wish to multiply \(2x^2-x+1\) by \(x+1\). Since \(x+1\) looks like this

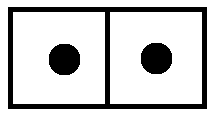
we need to replace each dot in the picture of \(2x^2-x+1\) with one-dot-and-one-dot, and each antidot with the anti-version of this, which is one-antidot-and-one-antidot. (This is now getting fun!)

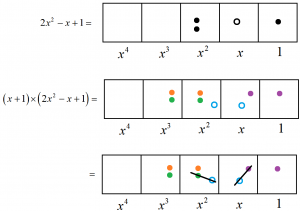
After some annihilations we see that \(\left(x+1\right) \times \left(2x^2-x+1\right)\) equals \(2x^{3}+x^2+1\).

Now let’s multiply \(2x^2-x+1\) with \(x-2\), which looks like this.

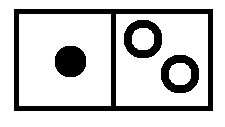
Each dot is to be replaced by one-dot-and-two-antidots, and each antidot with the opposite of this.

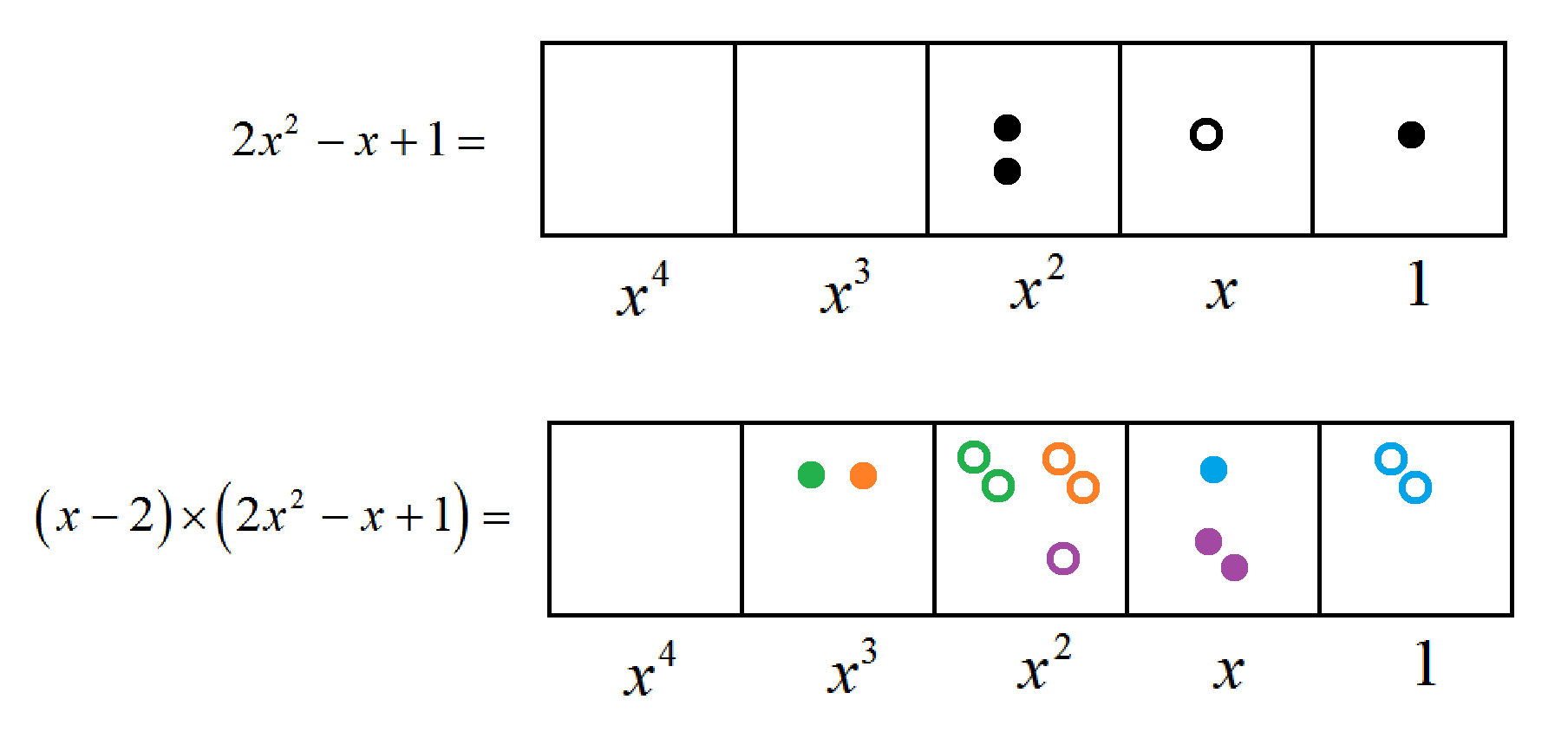
We see \(\left(x-2\right)\left(2x^2-x+1\right)=2x^{3}-5x^2+3x-2\).

Okay, you’re turn. Try \(2x^2-x+1\) times \(2x^2+3x-1\). Do you get this picture? (I’ve not colored it this time!) Do you see the answer \(4x^{4}+4x^{3}-3x^2+4x-1\)?

The process here is no different from the long multiplication of lesson 3.6, but one might have to contend with antidots now.

ADDING AND SUBTRACTING POLYNOMIALS

Adding and subtracting in base \(x\) is just like adding and subtracting in base \(10\). And it is easier in fact! Since we don’t know the value of \(x\) we will never explode dots. That is, we never need to perform “carries” as one does in base \(10\) arithmetic!

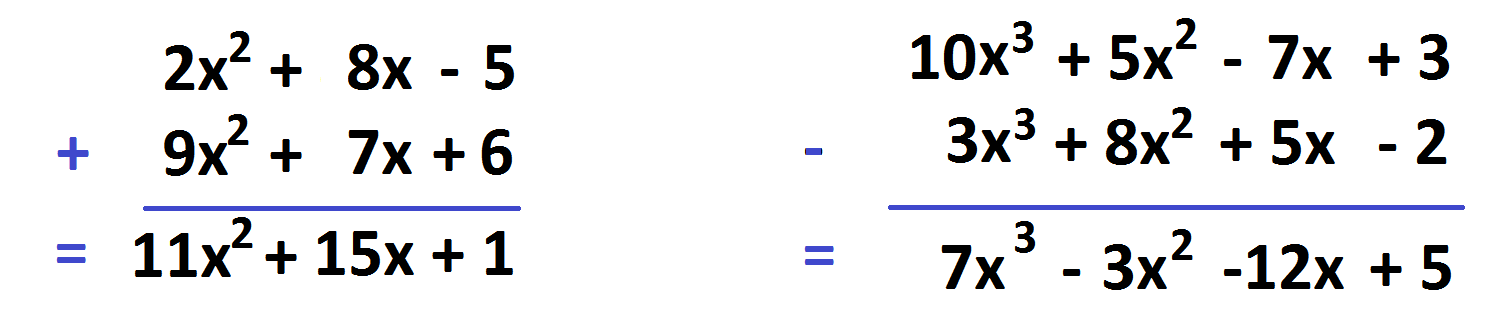
We can draw dots and boxes pictures of these in an \(1 \leftarrow x\) machine if we like.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources