Dani demonstrates this very polynomial division in a video.   

 

Consider again the \(1 \leftarrow x\) machine.

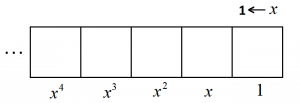
And let’s use this machine compute this strange division problem: \(\dfrac{1}{1-x}\). This is the very simple polynomial \(1\), which looks like this

divided by \(1-x\), which looks like this, one antidot and one dot.

 

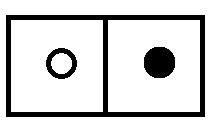
Do you see any one-antidot-and one-dot pairs in the picture of just \(1\)? Nope!

 

But remember

If there is something in life you want, make it happen! (And deal with the consequences.)

 

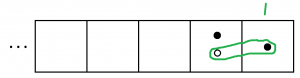
Can we make antidiot-dot pairs appear in the picture? Wouldn’t it be nice to have an antidot to the left of the one dot we have?

 

Well, make it happen!

 

And to keep that box technically empty we need to add a dot as well. That gives us one copy of what we want.

And we can do it again.

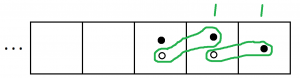
And again.

In fact, we can see we’ll be doing this forever!

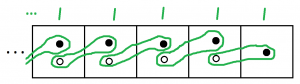
Whoa!

 

How do we read this answer?

 

Well, we have one \(1\), and one \(x\), and one \(x^2\), and one \(x^3\), and so on. We have

\(\dfrac{1}{1-x}=1+x+x^2+x^3+x^4+\cdots\)

 

The answer is an infinite sum.

 

 

The equation we obtained is a very famous formula in mathematics. It is called the geometric series formula and it is often given in many upper-level high school text books for students to use. But textbooks often write the formula the other way round, with the letter \(r\) rather than the letter \(x\).

\(1+r+r^2+r^3+\cdots=\dfrac{1}{1-r}\).

 

In a calculus class, one might say we’ve just calculated the Taylor series of the rational function \(\dfrac{1}{1-x}\). That sounds scary! But the work we did with dots-and-boxes shows that is not at all scary. In fact, it all kind of fun!

 

Here are some questions for you to try if you want. (And each question says what the answer should be!)

 

1. Use dots-and-boxes to show that \(\dfrac{1}{1+x}\) equals \(1-x+x^2-x^3+x^4-\cdots\) .

2. Compute \(\dfrac{x}{1-x^2}\). Do you get a sum of odd powers of \(x\)?

 

This next question is really cool! I advise you to draw very big boxes when you draw your dots and boxes picture. (The number of dots you need grows large quite quickly.)

 

3. Compute \(\dfrac{1}{1-x-x^2}\) and discover the famous Fibonacci sequence!

 

 

 

 

 

Resources