A fraction is a number that is an answer to a division problem. For example, the fraction \(dfrac{1}{8}\) is the result of dividing \(1\) by \(8\).  And we can compute \(1 \div 8\) in a \(1 \leftarrow 10\) machine by making use of decimals. The method is exactly the same as for division without decimals.

 

For \(1 \div 8\) we seek groups of eight in the following picture.

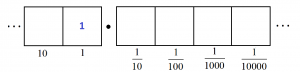
None are to be found right away, so let’s unexplode.

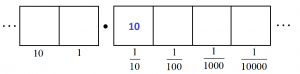
We have one group of 8, leaving two behind.

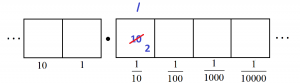
Two more unexplosions.

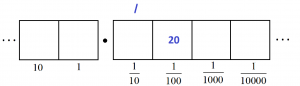
This gives two more groups of 8 leaving four behind.

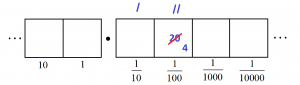
Unexploding again

reveals five more groups of 8 leaving no remainders.

We see that \(\dfrac{1}{8}\), as a decimal,  turns out to be \(0.125\). And as a check we have

 

\(0.125=\dfrac{125}{1000}=\dfrac{25}{200}=\dfrac{1}{8}\).

 

 

Here are some practice problems for you to pick and choose from.

 

18. Perform the division in a \(1 \leftarrow 10\) machine to show that \(\dfrac{1}{4}\), as a decimal, is \(0.25\).

19. Perform the division in a \(1 \leftarrow 10\) machine to show that \(\dfrac{1}{2}\), as a decimal, is \(0.5\).

20. Perform the division in a \(1 \leftarrow 10\) machine to show that \(\dfrac{3}{5}\), as a decimal, is \(0.6\).

21. Perform the division in a \(1 \leftarrow 10\) machine to show that \(\dfrac{3}{16}\), as a decimal, is \(0.1875\).

22. In simplest terms, what fraction is represented by each of these decimals?

        \(0.75\)     \(0.625\)     \(0.16\)     \(0.85\)     \(0.0625\)

 

Not all fractions lead to simple decimal representations. For example, consider the fraction \(\dfrac{1}{3}\). To compute it, we seek groups of three in the following picture.

Let’s unexplode.

We see three groups of 3 leaving one behind.

Unexploding gives another ten dots to examine.

We find another three groups of 3 leaving one behind.

And so on. We are caught in an infinitely repeating cycle.

 

This puts us in a philosophically interesting position. As human beings we cannot conduct this, or any, activity for an infinite amount of time. But it seems very tempting to write

 

\(\dfrac{1}{3}=0.3333\cdots\)

 

with the ellipsis representing the instruction “keep going with this pattern forever.” In our minds we can almost imagine what this means. But as a practical human being it is beyond our abilities: one cannot actually write down those infinitely many 3s represented by the ellipses.

 

Nonetheless, many people choose not to contemplate what an infinite statement like this means and just carry on to say that some decimals are infinitely long and not be worried by it.  In which case, the fraction \(\dfrac{1}{3}\) is one of those fractions whose decimal expansion goes on forever.

 

Notation: Many people make use of a vinculum (a horizontal bar) to represent infinitely long repeating decimals. For example, \(0.\overline{3}\) means “repeat the 3 forever”

\(0.\overline{3}=0.333\cdots\)

and \(0.38\overline{142}\) means “repeat the group 142 forever” after the beginning “38” hiccup:

\(0.38\overline{142}=0.38142142142142\cdots\).

 

As another (complicated) example, here is the work that converts the fraction \(\dfrac{6}{7}\) to an infinitely long repeating decimal. Make sure to understand the steps one line to the next.

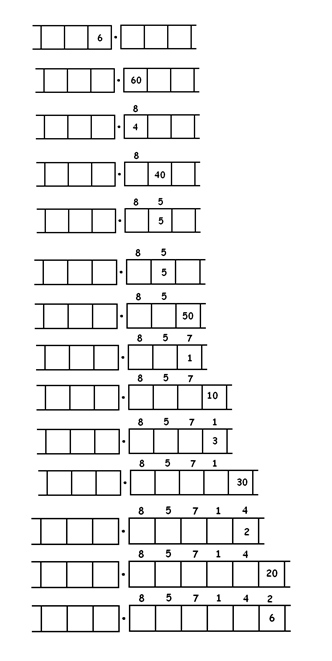
Do you see, with this 6 in the final right-most box that we have returned to the very beginning of the problem? This means that we shall simply repeat the work we have done and obtain the same sequence 857142 of answers, and then again, and then again. We have

 

\(\dfrac{6}{7}=0.857142857142857142\cdots\).

 

 

Some more practice questions if you like.

 

23. Compute \(\dfrac{4}{7}\) as an infinitely long repeating decimal.

24. Compute \(\dfrac{1}{11}\) as an infinitely long repeating decimal.

25. Which of the following fractions give infinitely long decimal expansions?

\(\dfrac{1}{2}\)     \(\dfrac{1}{3}\)     \(\dfrac{1}{4}\)     \(\dfrac{1}{5}\)     \(\dfrac{1}{6}\)     \(\dfrac{1}{7}\)     \(\dfrac{1}{8}\)     \(\dfrac{1}{9}\)     \(\dfrac{1}{10}\)

26. Use a \(1 \leftarrow 10\) machine to compute \(133 \div 6\), writing the answer as a decimal.

27. Use a \(1 \leftarrow 10\) machine to compute \(255 \div 11\), writing the answer as a decimal.

 

 

Resources