We have seen that fractions can possess finitely long decimal expansions. For example, \(\dfrac{1}{8}=0.125\) and \(\dfrac{1}{2}=0.5\).

 

And we have seen that fractions can possess infinitely long decimal expansion. For example, \(\dfrac{1}{3}=0.3333\cdots\) and \(\dfrac{6}{7}=0.857142857142857142\cdots\).

 

All the examples of fractions with infinitely long decimal expansions we’ve seen so far fall into a repeating pattern. This is curious.

 

We can even say that our finite examples eventually fall into a repeating pattern too, a repeating pattern of zeros after an initial start.

 

\(\dfrac{1}{8}=0.125000000\cdots = 0.125\overline{0}\)

\(\dfrac{1}{2}=0.500000000\cdots = 0.5\overline{0}\)

\(\dfrac{1}{3}=0.\overline{3}\)

\(\dfrac{6}{7}=0.\overline{857142}\)

 

This begs the question: Does every fraction have a decimal representation that eventually repeats?

The answer to this question is YES and our method of division explains why.

 

Let’s go through the division process again, slowly, first with a familiar example. Let’s compute the decimal expansion of \(\dfrac{1}{3}\) again in a \(1 \leftarrow 10\) machine. We think of \(\dfrac{1}{3}\) as the answer to the division problem \(1\div 3\), and so we need to find groups of three within a diagram of one dot.

We unexplode the single dot to make ten dots in the tenths position. There we find three groups of three leaving a remainder of 1 in that box.

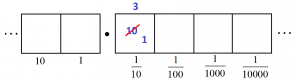
Now we can unexploded that single dot in the tenths box and write ten dots in the hundredths box. There we find three more groups of three, again leaving a single dot behind.

And so on. We are caught in a cycle of having the same remainder of one dot from cell to cell, meaning that the same pattern repeats. Thus we conclude \(\dfrac{1}{3}=0.333\cdots\). The key point is that the same remainder of a single dot kept appearing.

 

Here’s a more complicated example. Let’s compute the decimal expansion of \(\dfrac{4}{7}\) in the \(1 \leftarrow 10\) machine. That is, let’s compute \(4 \div 7\).

We start by unexploding the four dots to give 40 dots in the tenths cell. There we find 5 groups of seven, leaving five dots over.

Now unexplode those five dots to make 50 dots in the hundredths position. There we find 7 groups of seven, leaving one dot over.

Unexplode this single dot. This yields 1 group of seven leaving three remaining.

Unexplode these three dots. This gives 4 groups of seven with two remaining.

Unexplode the two dots. This gives 2 groups of seven with six remaining.

Unexplode the six dots. This gives 8 groups of seven with four remaining.

 

But this is predicament we started with: four dots in a box!

 

So now we are going to repeat the pattern and produce a cycle in the decimal representation. We have

 

\(\dfrac{4}{7}=0.571428  571428  571428  \cdots\).

 

Stepping back from the specifics of this problem, it is clear now that one must be forced into a repeating pattern. In dividing a quantity by seven, there are only seven possible numbers for a remainder number of dots in a cell – 0, 1, 2, 3, 4, 5, or 6 – and there is no option but to eventually repeat a remainder and so enter a cycle.

 

In the same way, the decimal expansion of \(\dfrac{18}{37}\) must also cycle. In doing the division, there are only thirty-seven possible remainders for dots in a cell (0, 1, 2, …, 36). As we complete the division computation, we must eventually repeat a remainder and again fall into a cycle.

 

We have just established a very interesting fact.

 

ALL FRACTIONS HAVE A REPEATING DECIMAL REPRESENTATION.

 

(A repeating pattern of zeros is possible. In fact, as a check, conduct the division procedure for the fraction \(\dfrac{1}{8}\). Make sure to understand where the cycle of repeated remainders commences.)

 

This now opens up a curious idea:

 

A quantity given by a decimal expansion that does not repeat cannot be a fraction!

 

For example, the quantity

 

\(0.101100111000111100001111100000\cdots\)

 

is designed not to repeat (though there is a pattern to this decimal expansion) and so represents a number that is not a fraction.

 

A number that is equivalent to the ratio of two whole numbers (that is, a fraction) is called a rational number. A number that cannot be represented this way is called an irrational number.

 

It looks like we have just proved that irrational numbers exist! Not all numbers are fractions.

 

In fact, we can now invent all sorts of numbers that can’t be fractions! For example

\(0.102030405060708090100110120130140150\cdots\)

and

\(0.3030030003000030000030000003\cdots\)

are irrational numbers.

 

Of course, we have all heard that numbers like \(\sqrt{2}\) and \(\pi\) are irrational numbers. It is not at all obvious why they are and how you would go about proving that they are. (In fact, it took mathematicians about 2000 years to finally establish that \(\pi\) is an irrational number. Swiss mathematician Johann Lambert finally proved it so in 1761.) But if you are willing to believe that these numbers are irrational, then you can say for sure that their decimal expansions possess no repeating patterns!

Resources