As promised, here are my solutions to the questions posed.

 

1. “Six tenths” says exactly what the number is.

 

2. Indeed both students are correct. Performing some explosions on Subra’s picture gives JinJin’s picture. (And performing some unexplosions on JinJin’s picture gives Subra’s!)

 

3. a) B    b) C

 

4. We have, in order, \(\dfrac{1}{20}\), \(\dfrac{1}{5}\), \(\dfrac{4}{5}\), and \(\dfrac{1}{250}\).

 

5. We have, in order, \(\dfrac{4}{10}=0.4\), \(\dfrac{4}{100}=0.04\), \(\dfrac{5}{100}=0.05\), \(\dfrac{5}{1000}=0.005\), and \(\dfrac{8}{10000}=0.0008\).

 

6. a) B    b) D

 

7. In order, we have \(0.35\), \(0.64\), \(0.602\), \(0.34\), and \(0.75\).

 

8. a) As a mixed number it is \(2\dfrac{3}{10}\). Or we could write \(2+\dfrac{3}{10}=\dfrac{20}{10}+\dfrac{3}{10}=\dfrac{23}{10}\).

b) \(17+\dfrac{4}{100}=17\dfrac{1}{25}\).

c) \(1003\dfrac{1003}{10000}\).

 

9. a) Unexploding one dot in the tenths box does “add” ten dots to the hundredths box.

b) Unexploding one dot in the tenths box does now give us 19 dots in the hundredths box. Unexploding these gives 190 dots in the thousandths box.

c) There isn’t much to say here. One can see that one can convert any one picture to any other by explosions and/or unexplosions.

d) Yes! All the pictures are the same, so 0.19 and 0.190 are the same number.

 

10. a) \(5.3\)

b) \(7+\dfrac{2}{10}\)

c) \(13.5\)

d) \(106+\dfrac{15}{100}=106.15\)

e) \(3+\dfrac{3}{25}=3+\dfrac{12}{100}=3.12\)

f) \(2+\dfrac{1}{4}=2+\dfrac{25}{100}=2.25\)

g) \(3 + \dfrac{11}{40}=3+\dfrac{275}{1000}=3.275\)

 

11. \(0.05+0.006=0.056\) and \(0.05-0.006-0.0|5|-6=0.044\). Drawing the dots and boxes makes these answers clear.

 

12. If I draw dots and boxes, then I agree with Agatha.

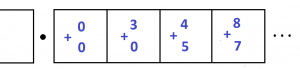
But I don’t agree with Percy.

 

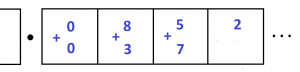
13. Multiplying by \(100\) is the same as multiplying by ten and then multiplying by ten again.

 

14. We have \(0.04 \times 0.5 = \dfrac{4}{100} \times \dfrac{5}{10}=\dfrac{20}{1000}=\dfrac{2}{100}=0.02\).

(We could have seen this right away too if we noted that \(0.5\) is a half, and one half of \(0.04\) is \(0.02\).)

 

We have \(1000 \times 0.0385=1000 \times \left(\dfrac{3}{100}+\dfrac{8}{1000}+\dfrac{5}{10000}\right)=30+8+\dfrac{5}{10}=38.5\).

 

15. We have \(\dfrac{0.9}{10}=\dfrac{9}{100}=0.09\).

We have  \(\dfrac{2.34}{1000}=\dfrac{1}{1000}\times \left(2+\dfrac{3}{10}+\dfrac{4}{100}\right)=\dfrac{2}{1000}+\dfrac{3}{10000}+\dfrac{4}{100000}=0.00234\).

We have \(\left(40+\dfrac{4}{100}\right)\times \dfrac{1}{100}=\dfrac{4}{10}+\dfrac{4}{10000}=0.4004\).

 

16. \(\dfrac{0.75}{25}=\dfrac{75}{2500}=\dfrac{3}{100}=0.03\).

 

17. This is technically a yes/no question, and the smart answer is no.

For those who answered yes, here are my approaches to the problems.

 

a) \(0.3 \times \left(5.37-2.07\right)=0.3\times \left(3.3\right) = \dfrac{3}{10}\times \left(3 +\dfrac{3}{10}\right)=\dfrac{9}{10}+\dfrac{9}{100}=0.99\)

 

b) \(\dfrac{0.1+\left(1.01-0.1\right)}{0.11+0.09}=\dfrac{0.1+\left(0.91\right)}{0.2}=\dfrac{1.01}{0.2}=\dfrac{101}{20}=\dfrac{505}{100}=5.05\)

 

c) \(\dfrac{\left(0.002+0.2\times 2.-02\right)\left(2.2-0.22\right)}{2.22-0.22}\)

\(=\dfrac{\left(0.002+0.404\right)\left(1.98\right)}{2}\)

\(=\dfrac{\left(0.406\right)\left(1.98\right)}{2}\)

\(=\dfrac{\left(\dfrac{4}{10}+\dfrac{6}{1000}\right)\left(1+\dfrac{9}{10}+\dfrac{8}{100}\right)\times 1000 \times 100}{2\times 1000 \times 100}\)

\(=\dfrac{\left(400+6\right)\left(100+90+8\right)}{2\times 1000 \times 100}\)

\(=\dfrac{406\times 198}{2\times 1000 \times 100}\)

\(=\dfrac{80388}{2\times 100000}\)

\(=\dfrac{40194}{100000}=0.40194\)

Whoa!

 

18. Do it!

 

19. Do it too!

 

20. Do it!

 

21. You guessed it. Do it!

 

22. In order, we have \(\dfrac{3}{4}\), \(\dfrac{5}{8}\), \(\dfrac{4}{25}\), \(\dfrac{17}{20}\), and \(\dfrac{5}{80}\).

 

23. We get \(\dfrac{4}{7}=0.571428 571428 571428 \cdots\).

 

24. We get \(\dfrac{1}{11}=0.09090909\cdots\).

 

25. The fractions \(\dfrac{1}{3}\), \(\dfrac{1}{6}\), \(\dfrac{1}{7}\), and \(\dfrac{1}{9}\) have infinitely long decimal expansions.

 

26 \(\dfrac{133}{6}-22.16666\cdots\).

 

27. \(\dfrac{255}{11}=23.18181818\cdots\).

 

28. Do it!

 

29. Do it too!

 

30. Yep, do it!

 

31. Let’s do all our writing in a \(1 \leftarrow 7\) machine. So the number seven is \(10\) and one less than this number is \(6\). Also, notice that multiplying a number by seven in a \(1 \leftarrow 7\) machine has the effect of addending a zero at the end of the number. (Can you see why? It is the same reason why multiplying by ten in a \(1 \leftarrow 10\) machine has the effect of addending a zero.) Multiplying by seven also “shifts the decimal point” one place.

 

Set \(0.333\cdots = x\).

 

Multiply each side by seven (which looks like \(10\)). This gives

 

\(3.3333\cdots = 10x\).

 

The left side is \(3+0.333\cdots\), that is, \(3\) plus the original number.

 

\(3+x=10x\)

 

Subtract \(x\) from both sides.

 

\(3=6x\)

 

So \(x\) must equal a half!

 

32. Can you see how to do it?

Resources