BASE NEGATIVE FOUR

A \(-1 \leftarrow 4\) machine operates by converting any four dots in one box into an antidot one place to the left (and converts four antidots in one box to an actual dot one place to the left).

a) This machine is a base machine:

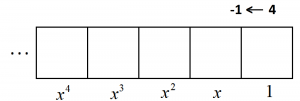
Explain why equals \(x=-4\).

b) What is the representation of the number one hundred in this machine? What is the representation of the number negative one hundred in this machine?

c) Verify that \(2|-3|-1|2\) is a representation of some number in this machine. Which number? Write down another representation for this same number.

d) Write the fraction \(\dfrac{1}{3}\) as a “decimal” in base \(-4\) by performing long division in a \(-1 \leftarrow 4\) machine.  Is your answer the only way to represent \(\dfrac{1}{3}\) in this base?

BASE NEGATIVE TWO

Consider a strange machine (invented by Dr. Dan V.) following the rule \(1|1|0 \leftarrow 0|0|2\). Here any pair of dots in a box are replaced by two consecutive dots just to their left.

 

Put in one dot and you get the code \(1\).

Put in two dots and you get the code \(110\).

Three dots give the code \(111\).

Four dots gives  \(112=220=1300=12100=120100=1200100=12000100=\cdots\). We have an infinite string.

 

a) Show that this machine is a base negative-two machine.

b) Show that one dot next to two dots anywhere in the machine have combined value zero.

 

Thus, in this machine, we can delete any \(1|2\)s we see in a code. Consequently, there is a well-defined code for four dots, namely, \(100\).

 

c) What are the \(1|1|0 \leftarrow 0|0|2\) machine codes for the numbers five through twenty?

 

Extra: Play with a \(1|1|0 \leftarrow 0|0|3\) machine. (What base is it?)

 

 

BASE PHI

Consider another strange machine, \(1|0|0 \leftrightarrow 0|1|1\). Here two dots in consecutive boxes can be replaced with a single dot one place to the left of the pair and, conversely, any single dot can be replaced with a pair of consecutive dots to its right.

Since this machine can move both to the left and to the right, let’s give it its full range of “decimals” as well.

a) Show that, in this machine, the number 1 can be represented as 0.10101010101…. (It can also be represented just as 1!)

b) Show that the number 2 can be represented as 10.01.

c) Show that the number 3 can be represented as 100.01.

d) Explain why each number can be represented in terms of 0s and 1s with no two consecutive 1s . (TOUGH: Are such representations unique?)

 

Let’s now address the question: What base is this machine?

 

e) Show that in this machine we need \(x^{n+2}=x^{n+1}+x^{n}\) for all \(n\).

f) Dividing throughout by \(x^{n}\) this tells us that \(x\) must be a number satisfying \(x^2=x+1\). There are two numbers that work. What is the positive number that works?

g) Represent the numbers 4 through 20 in this machine with no consecutive 1s. Any patterns?

 

Related Aside:

The Fibonacci numbers are given by: 1, 1, 2, 3, 5, 8, 13, 21, 34, ….

They have the property that each number is the sum of the previous two terms.

 

In 1939, Edouard Zeckendorf proved (and then published in 1972) that every positive integer can be written as a sum of Fibonacci numbers with no two consecutive Fibonacci numbers appearing in the sum.  For example

\(17=13+3+1\)

and

\(46=34+8+3+1\).

 

(Note that 17 also equals \(8+5+3+1\) but this involves consecutive Fibonacci numbers.)

 

Moreover, Zeckendorf proved that the representations are unique.

 

Each positive integer can be written as a sum of non-consecutive Fibonacci numbers in precisely one way.

 

This result has the “feel” of a base machine at its base.

 

Construct a base machine related to the Fibonacci numbers in some way and use it to establish Zeckendorf’s result.

 

Comment: Of course, one can prove Zeckendorf’s result without the aid of a base machine. (To prove that a number \(N\) has a Zeckendorf representation adopt a “greedy” approach: subtract the largest Fibonacci number smaller than \(N\) from it, and repeat. To prove uniqueness, set two supposed different representations of the same number equal to each other and cancel matching Fibonacci numbers. Use the relation \(F(n+2)=F(n+1)+F(n)\) to keep canceling.)

 

FINAL THOUGHTS

Invent other crazy machines …

 

Invent \(a|b|c \leftrightarrow d|e|f\) machines for some wild numbers \(a,b,c,d,e,f\).

 

Invent a base half machine.

 

Invent a base negative two-thirds machine.

 

Invent a machine that has one rule for boxes in even positions and a different rule for boxes in odd positions.

 

Invent a base \(i\) machine or some other complex number machine.

 

 

How does long division work in your crazy machine?

What is the fraction \(\dfrac{1}{3}\) in your crazy machine?

Do numbers have unique representations in your machines or multiple representations?

 

Go wild and see what crazy mathematics you can discover!

 

Resources