Permutations and Combinations
2.5 STEP THREE: The Labeling Principle
Lesson materials located below the video overview.
| In how many ways can we arrange the letters of the Swedish pop group name ABBA? |
Answer: \(\dfrac{4!}{2!2!} = \dfrac{24}{4} = 6\).
| In how many ways can we arrange the letters of AABBBBA? |
Answer: \(\dfrac{7!}{3!4!}\).
| In how many ways can we arrange the letters of AAABBBBCCCCCC? |
Answer: \(\dfrac{13!}{3!4!6!}\).
Let’s look at this third problem and phrase it in a different way:
| Mean Mr. Muckins has a class of 13 students. He has decided to randomly assign the grade of A to three students, the grade of B to four students, and the grade of C to six students. In how many ways could he assign these labels? |
Answer: Let’s imagine all thirteen students are in a line.
Here’s one way he can assign labels:
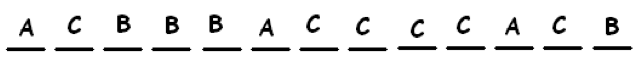
Here’s another way:
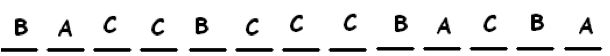
and so on.
We see that this labeling problem is just the same problem as rearranging letters. The answer must be \(\dfrac{13!}{3!4!6!}\).
| Of 10 people in an office 4 are needed for a committee. How many ways? |
Answer: Imagine the 10 people standing in a line. We need to give out labels. Four people will be called “ON” and six people will be called “LUCKY.” Here is one way to assign those labels:
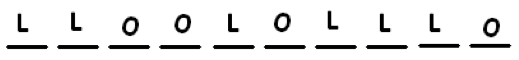
We see that this is just a word arrangement problem. The answer is:
\(\dfrac{10!}{4!6!}=\dfrac{10 \cdot 9 \cdot 8 \cdot 7}{4 \cdot 3 \cdot 2 \cdot 1} = 10 \cdot 3 \cdot 7 = 210\).
In general, we have …
| THE LABELING PRINCIPLEEach of \(N\) distinct objects is to be given a label. If \(a\) of them are to have label “1,” \(b\) of them to have label “2,” and so on, then the total number of ways to assign labels is:
\(\dfrac{N!}{a!b! \cdots z!}\). |
That’s it. We are just arranging letters, with the letters being the names of the labels.
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()


