Examples show how the multi-stage thinking works when it is needed.

 

Example: There are 7 men and 6 women in an office. How many ways are there to make a committee of five if …a)    Gender is irrelevant?b)    The committee must be all male?c)     The committee must consist of 2 men and 3 women?

 

Answer: a) This is just a problem of assigning labels to 13 people: five are “ON” and eight are “OFF.” There are:

\(\dfrac{13!}{5!8!} = \dfrac{13 \cdot 12 \cdot 11 \cdot 10 \cdot 9}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 13 \cdot 11\cdot 9 = 1287\)

ways to make the committee.

 

b) This is a problem just among the men: 7 people to be labeled. There are \(\dfrac{7!}{5!2!}=21\) committees.

 

c) THIS IS A TWO TASK PROBLEM!

 

Task 1: Deal with the men.

 \(\dfrac{7!}{2!5!} = 21\) ways

Task 2: Deal with the women

 \(\dfrac{6!}{3!3!} = 20\)  ways

 

By the multiplication principle, there are \(21 \times 20 = 420\)  ways to form the committee.

 

Example: A company would like to send out a team of five plumbers to a construction site. They will send two expert plumbers and three trainee plumbers. If there are a total of 10 expert plumbers available and 8 trainees, how many different teams are possible?

 

Answer: This too is a two task process:

 

Task 1: Select the experts

There are \(\dfrac{10!}{2!8!}\) possible ways to label two expert plumbers as “chosen” and the rest “not chosen.”

Task 2: Select the trainees

There are \(\dfrac{8!}{3!5!}\) possible ways to label three trainees as “chosen” and the rest “not chosen.”

 

By the multiplication principle, there are thus \(\dfrac{10!}{2!8!} \times \dfrac{8!}{5!3!}\) possible teams.

 

 

COMMENT: Notice that we have no control over who is labeled “expert” and who is labeled “trainee.” We only have control over the labels “chosen” and “not chosen.” That there are some fixed previously assigned labels is a hint that one might be contending with a multi-stage problem.

  

Example: There are:

20 Americans

10 Australians (which includes me, James.)

10 Austrians

 

Fourteen are needed for a math team. How many ways if …

 

a)    Nationality is irrelevant?

b)    The team must be all American?

c)     The team must have 5 Americans, 5 Australians, and 4 Austrians?

d)    Nationality is irrelevant, but I must be on the team?

 

Answer:

a)  \(\dfrac{40}{14!26!}\)    (Do you see why?)

 

b)  \(\dfrac{20!}{14!6!}\)   (Do you see why?)

 

c) Deal with Americans: \(\dfrac{20!}{5!15!}\).  Deal with the Australians: \(\dfrac{10!}{5!5!}\).  Deal with the Austrians: \(\dfrac{10!}{4!6!}\).

By the multiplication principle there are a total of  \(\dfrac{20!}{5!15!} \times \dfrac{10!}{5!5!} \times \dfrac{10!}{4!6!} \) ways to make a team.

 

d)  With me on the team for sure, the problem now is to select 13 more team members from 39 people. There are \(\dfrac{39!}{13!26!}\) ways to do this.

 

Example: In how many ways can one arrange the letters AMERICA …

a)    if there are no restrictions?

b)    if the rearrangement must begin with M?

c)     if the rearrangement must begin with M and end with C?

d)    if the rearrangement must begin with A?

 

Answer: a)  \(\dfrac{7!}{2!}\)  (Why?)

 

b) This is just a matter of arranging the letters AERICA in six slots:

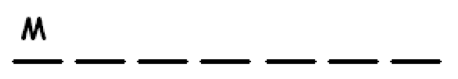
There are  \(\dfrac{6!}{2!}\) ways.

 

c) This is a matter of arranging the letters AERIA in five slots:

There are \(\dfrac{5!}{2!}\) ways.

 

d) We need to arrange the letters MERICA in six slots:

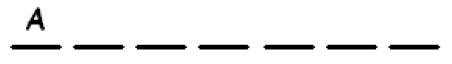
 There are \(6!\) ways.

 

 

 

There is often more than one way to think through a challenge.

 

Example: In how many ways can one arrange the letters of the word ORANGE if the first and last letters must each be a vowel?

 

Here vowels are given a different status to consonants. This means we likely need to think of this problem in stages.

 

Approach 1: 

Task 1: Deal with the vowels.

For the three vowels,  one will be labeled “in first position,” one as “in the last position” and one as “in with the consonants. There are \(\dfrac{3!}{1!1!1!} = 6\) ways to do this.

Task 2: Deal with consonants.

We have three consonants and the extra vowel acting as a consonant. We need to label them as in position 2, in position 3, in position 4 and in position 5. There are \(\dfrac{4!}{1!1!1!1!} = 24\) ways to do this.

 

By the multiplication principle there are thus \(6 \times 24 = 144\) possible desired arrangements.

 

Approach 2:

Think of this as a six task process: Deal with the first letter, deal with the last letter, then deal with the second, third, fourth and fifth letters. This gives the diagram:

 

EXAMPLE: In how many ways can one arrange the letters ABCDE so that A is not at the beginning nor the end?

 

Approach 1:  Think of this as a five-stage process! Deal with the first letter, deal with the last letter, deal with the second letter, deal with the third letter, and deal with the fourth letter. By the multiplication principle, we multiply the results.

   

 

Approach 2: The letters B, C, D, E have a different status than A.

 

Task 1: Place the letter A

There are 3 possible locations for this letter

Task 2:  Place the remaining letters

 There are four remaining positions for four letters. They can be placed in these positions \(\dfrac{4!}{1!1!1!1!} = 24\)  ways.

 

Thus there are \(3 \times 24 = 72\) possible desired arrangements.

 

 

Approach 3: There are five slots in which to place letters with the two end slots having a different status than the middle three.

 

Task 1: Fill the end slots.

There are four letters to work with, yielding \(\dfrac{4!}{1!1!2!} = 12\) possibilities. (The labels here are “first slot,” “last slot” and “not used.)

 

Task 2: Fill the middle three slots

There are three letters to work with yielding \(\dfrac{3!}{1!1!1!} = 6\) possibilities.

 

By the multiplication principle we have \(12 \times 6 = 72 \) permissible arrangements.

 

 

 

SOME PRACTICE:

All the answers appear in the COMPANION GUIDE to this Permutations and Combinations course.

 

Exercise 25: A committee of five must be formed from five men and seven women.

a)    How many committees can be formed if gender is irrelevant?

b)    How many committees can be formed if there must be at exactly two women on the committee?

c)     How many committees can be formed if one particular man must be on the committee and one particular woman must not be on the committee?

d)    CHALLENGE: How many committees can be formed if one particular couple (one man and one woman) can’t be on the committee together?

 HINT: Sometimes it is easier to count the opposite of what you want first!

 

The next four questions require some clever thinking. Have fun with them!

 

Exercise 26: There are:

20 Americans

10 Australians (which includes me, James.)

10 Austrians

 Fourteen are needed for a math team. How many possible teams include me whenever an American is on the team?

 

Exercise 27:a)    Twelve white dots lie in a row. Two are to be coloured red. In how many ways can this be done?

b)    Consider the equation \(10 = x + y + z\). How many solutions does it have if each variable is to be a positive integer or zero?

 

Exercise 28:  An ice-cream stand offers the “mega-bowl special:” twelve-scoops in a bowl from a choice of twelve possible flavors. How many different mega-bowl combinations does it offer?

 

COMMENT: The problem here is that scoops are indistinguishable.  Moreover, you are not told how many scoops there are to be of a particular label (flavor). Problems like these are hard and fall under the category of what is called “multi-choosing.”

 

HINT: Exercise 27 answers the following question; Ten scoops of ice-cream sit in a bowl with each scoop one of three possible flavors. How many possibilities can occur?

 

Exercise 29: Consider the question: In how many different ways can 8 people sit around a round table?

This is a vague question. What does “different” mean?

 

a)    Answer the question if the chairs of the table are marked North, Northeast, East, Southeast, South, …, Northwest.

b)    Answer the question if the chairs are not marked so that two different rotations of the same arrangement of people would be considered the same.

c)     Answer the question under the assumption that rotations are considered the same and reflections about a diameter of the table are considered the same.

 

Suppose two particular people must not sit next to one another. Answer each of the questions a), b) and c) with this added restriction.

(HINT: First count the number of arrangements with that couple seated together.)

 

 

 

Resources