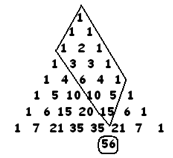
Sum all the entries in the parallelogram. (In this case we have: 15 + 10 + 5  + 6 + 4 + 1 + 3 + 3 + 1 + 1  + 2 + 1 + 1 + 1 + 1.) The answer is one less than the value of the entry directly below the circled entry two rows down. (In this case, one less than 56.)

a)    Play with this. Can you see why 56 is one more than the sum of entries in the parallelogram? (A yes/no answer will suffice.)

HINT: Think of the entries in the parallelogram as a series of parallel stockings.

b)    Can you see that this parallelogram property always works? (Again an honest yes or no will suffice.)

a)    How many times will the term \(y^{7}\) appear?

b)    How many times will the term \(xz^{6}\)  appear?

c)    How many times will the term \(x^{2}y^{3}z^{2}\) appear?

d)    Write a formula for the number of times a general term \(x^{a}y^{b}z^{c}\) will appear.

e)    State the general “trinomial theorem:”

\(\left(x+y+z\right)^{n}=\)

f)     State a general “quadronomial” theorem:

\(\left(x+y+z+w\right)^{n}=\)

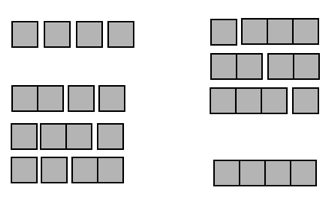
She also noticed that there is 1 train using four blocks, 3 using three blocks, 3 using two blocks and 1 using one block.

a)    Draw all the trains of length five Sally can make. Group them according to the number of blocks in each train.

b)    Why the connection to Pascal’s triangle?