Permutations and Combinations
3.8 Still Yet More Practice!
All solutions appear in the COMPANION GUIDE to this Permutations and Combinations course.
| Exercise 42: Physicists often say that \((1+h)^{n}\) is approximately \(1+nh\) if \(h\) is small. What makes them think this?HINT: If \(h\) is small, then \(h^{2}\) is negligible. |
| Exercise 43: The labeling principle shows that there are \(\dfrac{n!}{k!(n-k)!}\) ways to select \(k\) objects from a collection of \(n\) objects. (Label the objects either as “chosen” or “not chosen.”) Thus the binomial coefficient \({n \choose k}\) is the answer to a choosing problem.Let \(\left({n \choose k}\right)\) represent the answer to a different type of choosing problem:In how many ways can one select \(k\) objects if there are \(n\) different types of objects to choose from and one may select the same object multiple times?
For example, \(\left({2 \choose 3}\right) = 4 \) since there are four ways to select three objects of two possible types A or B, namely, AAA, AAB, ABB, and BBB.
a) Check that \(\left({3 \choose 3}\right) = 10 \) and \(\left({3 \choose 5}\right) = 21 \). b) Compute \(\left({3 \choose 1}\right)\), \(\left({3 \choose 2}\right)\) and, \(\left({3 \choose 0}\right)\) . c) Draw a table of \(\left({n \choose k}\right)\) values for n = 1, 2, 3 and for k = 0, 1, 2, 3. What do you notice? d) Show that \(\left({n \choose k}\right) = {a \choose b} \) for some appropriate values of \(a\) and \(b\). (What values?) |
Exercise 44: Consider the first eight rows of Pascal’s triangle:
a) Circle the odd entries in the diagram above. b) Which entries will be odd in the next row of the triangle? c) Draw a picture showing the location of the odd entries of the first 20 rows of Pascal’s triangle? d) Which rows of Pascal’s triangle have entries that are all odd? Can you explain why what you are claiming is true? |
Exercise 45: Choose any interior entry of Pascal’s triangle and consider its six surrounding entries making a hexagon of numbers.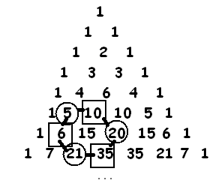 Take the product of alternating entries in this hexagon. Take the product of alternating entries in this hexagon.
\(5 \times 20 \times 21 = 2100\) \(10 \times 35 \times 6 = 2100\) These products are equal.
a)Test this out. Choose another entry of Pascal’s triangle and compute the two alternating products. Test it out a second time.
b) Prove that the alternating products in a hexagon from Pascal’s triangle will always equal.
HINT: Suppose the interior entry you choose is \(\dfrac{n!}{k!(n-k)!}\). Write down the formulas for its six neighbours. Do the algebra to show that the alternating products are always equal.
OPTIONAL HARD CHALLENGE: Suppose the numbers in a hexagon, in turn,are \(a_{1}\), \(b_{1}\),\(a_{2}\), \(b_{2}\), \(a_{3}\), and \(b_{3}\). Prove that the greatest common divisor of the alternating terms are sure to be equal: \( gcd(a_{1}, a_{2}, a_{3}) = gcd(b_{1}, b_{2}, b_{3}) \) .
[In our example \(gcd(5, 20, 21) = 1\) and \(gcd(10, 35, 6) = 1\).] |
Exercise 46: a) How many paths are possible from S to E if, along with right steps (R) and down steps (D), southeast diagonal steps (X) are now permitted.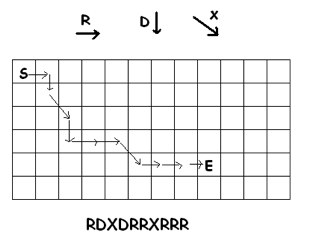
b) Fill in the grid of squares with numbers showing the number of paths from S to each cell. Any patterns?
c) Write a formula for the number of paths from S to the cell in row \(a\) and column \(b\) (starting the count of the rows and columns at zero). |
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()


