Let’s start with a tiny puzzle:

There are three major highways from Adelaide to Brisbane, and four major highways from Brisbane to Canberra.

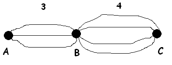
How many different routes can one take to travel from Adelaide to Canberra, always moving eastward in this diagram?

 

THINKING MOMENT: Is the answer \(7\)  from  \(3 + 4\),  or is the answer \(12\) from \(3 \times 4\)? Is addition or multiplication appropriate here?

 

One way to think of this is to say that for each choice of route from \(A\) to \(B\) – top, middle, or bottom – there are four choices with which to complete the journey to \(C\). We thus have a total of \(4+4+4\) possible journeys: three groups of four. This repeated addition (which is multiplication for counting numbers) shows that multiplication, \(3 \times 4\), is the appropriate answer. The are a total of \(12\) possible routes from \(A\) to \(C\).

 

Let’s take the puzzle up a notch:

Suppose there are also six major highways from Canberra to Darwin.

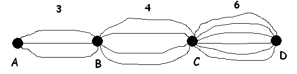
How many different routes are there from \(A\)  to \(D\)?

 

Be very clear in your mind that the answer is appropriately given by multiplication: \(3 \times 4 \times 6 = 72\) . (For each of the twelve routes from \(A\) to \(C\), we have six options for completing the journey. That’s twelve groups of six.)

 

Exercise 1: I own five different shirts, four different pairs of trousers and two sets of shoes. How many different outfits could you see me in?

 

Exercise 2: There are ten possible movies I can see and ten possible snacks I can eat while at the movies. I am going to see a film tonight and I will eat a snack. How many choices do I have in all for a movie/snack combo?

 

All the answers to exercise problems appear in the COMPANION GUIDE to this Permutations and Combinations course. 

 

We have a general principle:

THE MULTIPLICATION PRINCIPLE:  If there are \(a\) ways to complete a first task and  \(b\) ways to complete a second task, and no outcome from the first in any way affects a choice of outcome from the second, then there are \(a \times \b)  ways to complete both tasks as a pair.

 

This principle readily extends to the completion of more than one task.

 

Exercise 3: Explain the clause stated in the middle of the multiplication principle. What could happen if different outcomes from the first task affect choices available for the second task? Give a concrete example.

                                                                                   

EXAMPLE: On a multiple choice quiz there are five questions, each with three choices for an answer:

I decide to fill out my answers randomly. In how many different ways could I fill out the quiz? 

Answer: This is a five-task process:

Task 1: Answer question one:  \(3\)ways

Task 2: Answer question two:  \(3\) ways

Task 3: Answer question three:  \(3\) ways

Task 4: Answer question four:  \(3\) ways

Task 5: Answer question five:  \(3\) ways

 By the multiplication principle there are \(3 \times 3 \times 3 \times 3 \times 3 = 3^{5}\)  ways to complete the quiz.

 

That’s all there is to say about this first step to counting!

 

SOME PRACTICE:

Again, all the answers are in the COMPANION GUIDE to this course.

Exercise 4: A multiple choice quiz has 10 questions each with 4 different possible answers. In how many ways can one fill out the quiz?

 

Exercise 5: Ten people are up for election. In how many ways can one fill out a ballot for “president” and for “vice president”?

 

Exercise 6: In how many ways can I arrange six people in a line?

 

Exercise 7: In how many ways can one write down three vowels in order from left to right? How does the answer change if we insist that the vowels all be different?

 

Exercise 8: How many different paths are there from \(A\)  to \(G\)?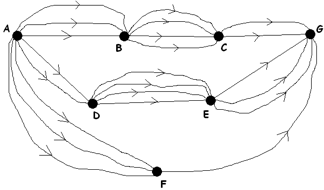

 

Resources