When we discover negative numbers we naturally, without question even, assume they obey the same laws of arithmetic as the ordinary positive counting numbers. That is, we like to believe that basic laws such as \(a\times b=b\times a\) and \(a \times 1=a\) and \(a \times 0=0\) hold for all numbers, both positive and negative, and that we can expand brackets even with negative entries, and so on. Of course, these rules assume we know a priori know how to multiply with negative numbers.

MULTIPLYING POSITIVE AND NEGATIVE NUMBERS

In the early curriculum multiplication is introduced in the context of whole counting numbers and is appropriately defined there as repeated addition. For instance, \(4 \times 5\) is read as “four groups of five” and is computed as such: \(4 \times 5 = 5 + 5 + 5 + 5 = 20\).

It is actually quite a surprise that \(5 \times 4\), “five groups of four,” gives the same numerical answer as four groups of five. The computation is quite different with the numbers 5 and 4 serving switched roles.

 

Question: How would you convince a young student that 193 groups of 307 is sure to have the same value as 307 groups of 193? Why do we wish that believe that \(a \times b = b \times a\) for counting numbers? (HINT: Put dots in rectangular arrays.)

 

Repeated addition allows us to multiply a positive number and a negative number. For example, \(2 \times \left(-3\right)\) can be read as “two groups of negative three” and so is computed as \(2 \times \left(-3\right)=-3+\;-3=-6\). Using piles and holes this looks like:

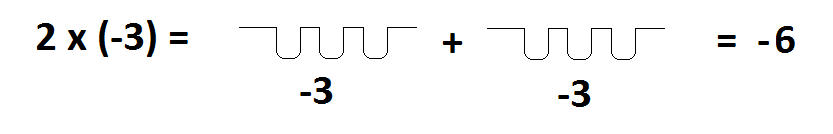
Interpreting negative times a positive and negative times negative through repeated addition, however, is problematic.

What could \(\left(-2\right) \times 3\) mean? “Negative two groups of three” makes no sense.

And \(\left(-2\right) \times \left(-3\right)\) is equally strange: “negative two groups of negative three.”

 

The truth is that multiplication has no meaning here in context of repeated addition. We have entered new territory and if we want to open up our world to new types of numbers it is not surprising that previously concrete, literal definitions begin to flail. So we have to engage in a sophisticated shift of thinking, letting go of the question What is multiplication? to ask instead:

How would we like multiplication to behave? 

 

Comment: Let me stress this point. Asking “What does the multiplication of negative numbers mean?” is a misleading question and it is not the question to ask at this point of our work: we’re still just trying to grapple with the issue of what multiplication is in the world of negative numbers could be. To approach this we first have to be clear on what features of arithmetic we feel should still be true.

 

THINKING OUR WAY THROUGH THINGS

Positive times Negative:  It does seem compelling to hold on to the “repeated addition” notion for the product of a negative and a positive:

\(2\times \left(-3\right)=\) two groups of negative three \(=-3+-3=-6\).

Most people agree we should stay with this idea.

 

Negative times Positive: This is problematic: \(\left(-2\right)\times 3=?\)

But it does seem compelling to say that the commutative law, \(a \times b = b\times a\), should hold for all types of numbers, including negative numbers. In which case we can write:

\(\left(-2\right)\times 3 =3\times \left(-2\right)\) three groups of negative two \(=-2+-2+-2=-6\).

 

Negative times Negative: How should we compute \(\left(-2\right) \times \left(-3\right)\)?

Applying the commutative law and thinking of this as \(\left(-3\right) \times \left(-2\right)\) does not help in this case. So what mathematics could guide us in our thinking here?

We did say that we like to believe that all the usual laws of arithmetic ( \(a\times b=b\times a\), \(a \times 1=a\) , \(a \times 0=0\), expanding brackets, and so on) should hold for all types of numbers. As the area model is just a representation our belief in expanding brackets, the area model should hold for negative numbers too!

KEY EXAMPLE: Here are three ways to compute \(17\times 18\) thinking of  \(17\) as either \(10+7\) or  \(20+\left(-3\right)\) and \(18\) as either \(10+8\) or \(20 + \left(-2\right)\). Even though geometrically it makes no sense to have a negative side length in a geometric figure, we see that the mathematics each diagram represents is still correct mathematics.

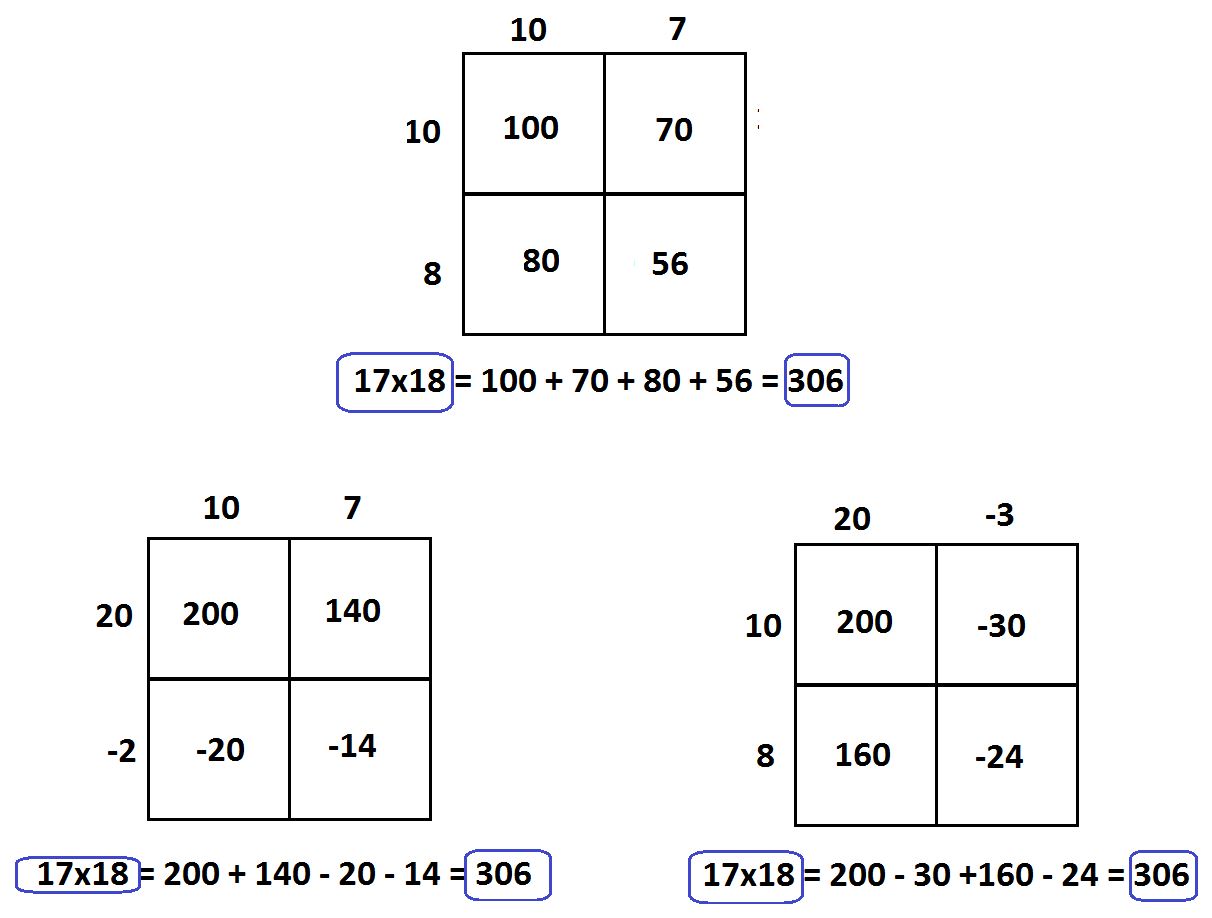
But there’s a fourth possible picture! 

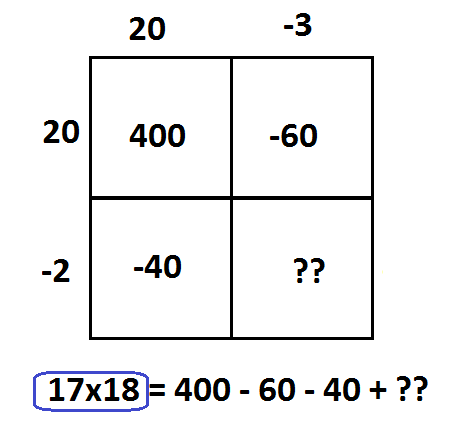
The mathematics of expanding brackets suggests that the the correct value of \(\left(-2\right)\times\left(-3\right)\) is \(+6\). (The product should still have answer \(306\).)

 

EXERCISE: Draw four diagrams representing \(26\times 35\) and use the final one to demonstrate why we should set \(\left(-4\right)\times\left(-5\right)=+20\).

 

THE PRECISE LOGICAL ARGUMENT AS TO WHY NEGATIVE TIMES NEGATIVE SHOULD BE POSITIVE

 

Once we agree that \(2\times\left(-3\right)=-6\)  (via repeated addition) and \(\left(-3\right)\times 2=-6\) (via a belief in commutativity), that negative times negative is positive is a forced logical consequence of these next two basic beliefs of arithmetic: \(a\times 0 = 0\) and \(a\left(b+c\right)=ab+ac\). Here’s why:

 

We’ll prove \(\left(-2\right)\times\left(-3\right)=+6\).

 

By the first of the rules we must say: \(\left(-2\right)\times 0 = 0\).

By rewriting the first zero we must then agree that: \(\left(-2\right)\times \left(3+\left(-3\right)\right) = 0\).

By distributing we must also agree that: \(\left(-2\right)\times 3 + \left(-2\right)\times\left(-3\right)=0\).

This reads: \(-6 + \left(-2\right)\times\left(-3\right)=0\).

It follows that \(\left(-2\right)\times\left(-3\right)\) must be \(+6\).

 

EXERCISE: Create a similar argument to establish that \(\left(-4\right)\times\left(-5\right)=+20\).

 

SO… WHAT IS MULTIPLICATION?

 

In the context of positive whole numbers it is repeated addition.

 

In the context of positive and negative whole numbers, I personally don’t know what it is, other than a mathematically consistent operation set so that if \(a\) and \(b\) are positive whole numbers, then \(a\times \left(-b\right)=-ab\), and with the logical consequences \(\left(-a\right)\times b = b \times \left(-a\right)=-ab\) and \(\left(-a\right)\times\left(-b\right) = ab\).

 

People try to give concrete meaning to all this with models of soldiers marching on number lines turning different directions, systems of profit and debt, working with temperatures above and below freezing, and so on. Each model is good for illustrating SOME aspect of the arithmetic of negative numbers, but not all. For example, the idea of “taking away five degrees of cold is the same as adding five degrees of warmth” might work for some to explain why \(-\left(-5\right)\) should equal \(5\), but it is not explaining in, and of itself, why negative times negative is dubbed positive.

 

Pedagogically we need to move away from starting student thinking about negative number multiplication with models that try, but must fail at some point, to “explain” what negative number multiplication is. We must start instead with a discussion on what we think should be true about multiplication in general and how it behaves. Expanding brackets, via the area model, gives a convincing student illustration that mathematics “wants” negative times negative to be positive. (And for students ready for it, the axiomatic approach clinches it.) As to what “negative times negative is positive” actually means – I don’t have a clue. I just know it is algebraically consistent.

 

EXERCISE: a) Prove that \(-a\) and \(\left(-1\right) \times a\) are the same number. (HINT: \(a+\left(-1\right)\times a = 1\times a + \left(-1\right)\times a = \ldots\) .)

b) If you believe that \(-\left(-5\right) = 5\) explain why it now follows that \(\left(-1\right) \times \left(-1\right) = 1\).

 

Resources