The Astounding Power of Area
1.7 A Brief Discussion on FRACTIONS
The subject of fractions throughout the K-12 curriculum is thorny (see my essay Why Fractions are Hard for a full account of their troubled woes in school mathematics) and I am a tad hesitant to present here just a brief overview of one aspect of fraction thinking – their use of the area model. This material should be a full course unto itself so that the subtleties and difficulties of fraction thinking are made explicit and clear to all educators. I will fail to attend to the topic with the care it deserves below.
Please regard the following simply as an overview of how area is used to illustrate some aspects of fraction work in the K-8 curriculum. (And please do read Why Fractions are Hard for the proper context of this work.) Little or no proper mention will be made of number-line thinking and fractions as solutions to division problems.
FRACTIONS: A TYPICAL FIRST APPEARANCE
Fractions are usually first introduced to youngsters as division by sharing:
A half a pie is the result of dividing a pie into two equal pieces.
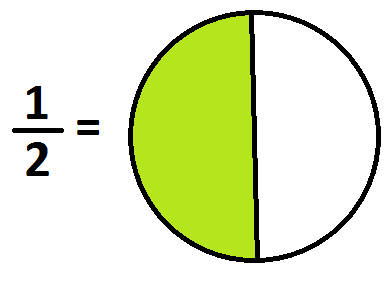
(It is presumed that the other piece of the pie has been shuffled elsewhere.) One draws pictures for a third of a pie, and a quarter of a pie, and so on, similarly:
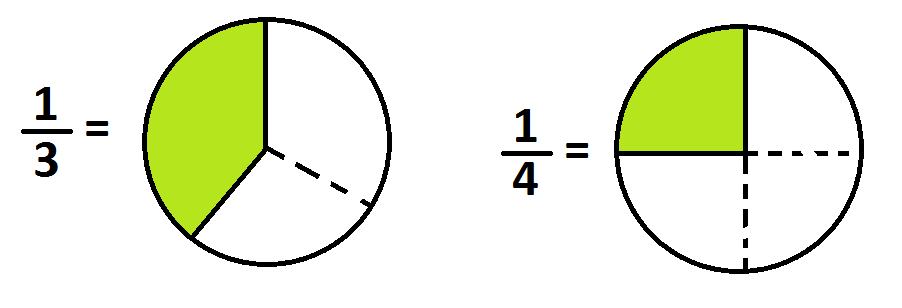
These pictures can be seen as the results of sharing: If we divide a pie equally between three people, then each person gets a piece of pie that looks like the left picture just above.
Comment: The language “parts of a whole” is often introduced too: each act of sharing does give a part of some whole. At first the whole is usually a pie, but it could also be pizza, or a baguette, or a group of kittens, or a section of yarn.
People usually draw round pies, but square- or rectangular-shaped pies are easier to draw and to think with.
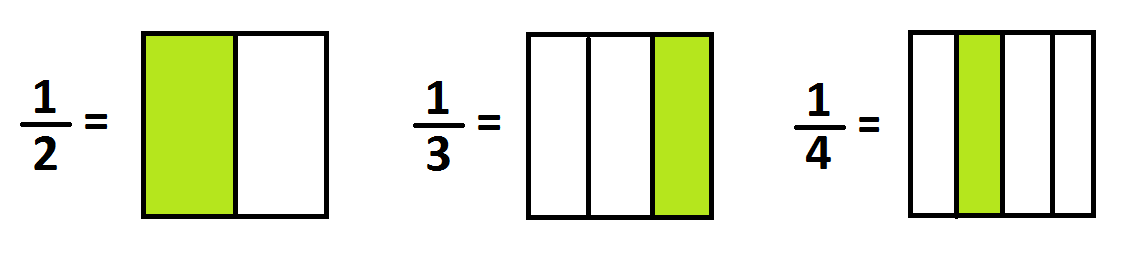
Of course one can draw pies of any shape one likes, or work with objects other than pie. For example, here is a picture of half a boy!
Question: Would it have been better to draw a vertical line divide the boy into two halves? (Maybe I was focusing on the height of the boy, not his volume.)
If we decide to divide unit line segments, then there is a natural place for these fractions on the number line. Here’s half a line segment:
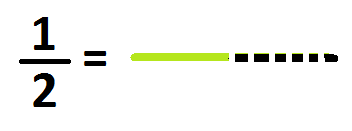
and here is the matching point on the number line:
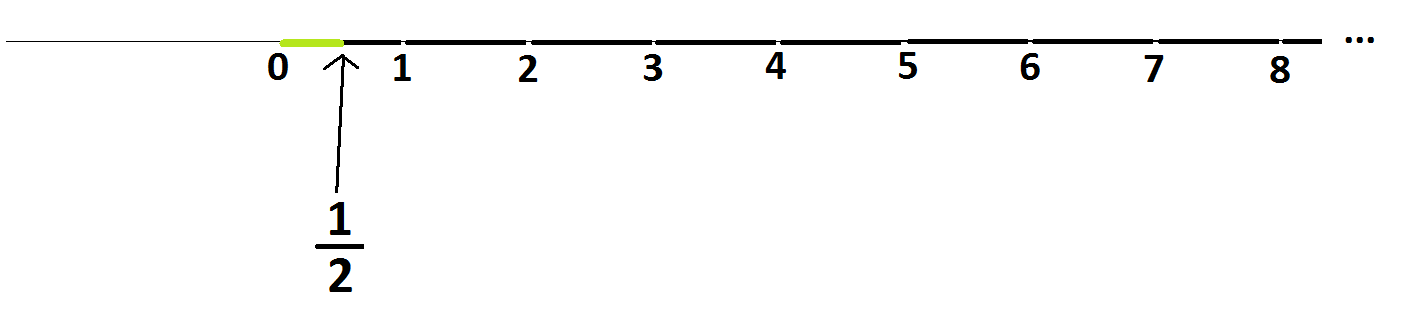
Many curriculums now are using the number line as the chief model for introducing fractions to students.
PUSHING THE “SHARING” MODEL FURTHER:
Let’s share more than one pie.
Suppose \(6\) pies, say, are to be shared equally among \(3\) boys. This clearly yields two pies per boy.
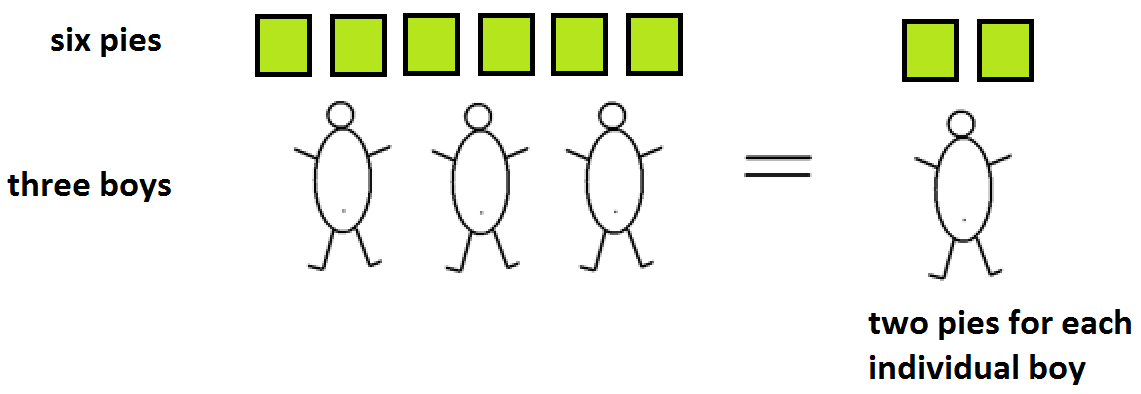
We write:
\(\dfrac{6}{3}=2\).
We might also write \(6 \div 3=2\) .
Comment: Notice that the obelus \(\div\) is derived from fraction notation \(\frac{a}{b}\).
Comment: Using boys in this model is fun, concrete, and pedagogically helpful, but actually immaterial. By \(\frac{6}{3}\) we actually mean “the result of sharing six pies three ways.” The answer is a quantity of pie, the quantity per share, which in this case is \(2\) pies.
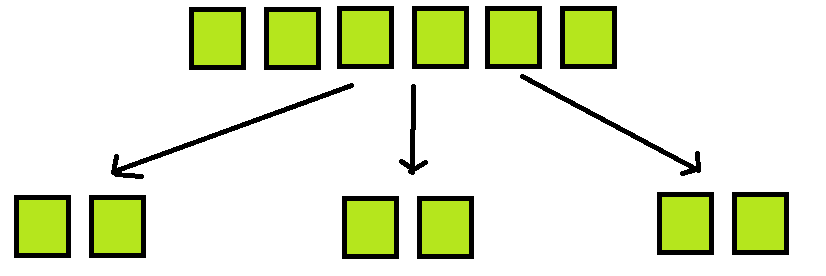
We could draw pictures without the boys if we like, but drawing boys is fun and motivating. We just need to keep in mind that our answers to sharing problems are always actual amounts of pie (and these amounts can be shared again, if we so wish!)
In this context …
sharing \(10\) pies among \(2\) boys yields \(\frac{10}{2}=5\) pies (per boy),
sharing \(8\) pies among \(2\) boys yields \(\frac{8}{2}=4\) pies,
sharing \(5\) pies among \(5\) boys yields \(\frac{5}{5}=1\) pie,
and
the answer to sharing \(1\) pie among \(2\) boys is \(\frac{1}{2}\), which we call “one half.”
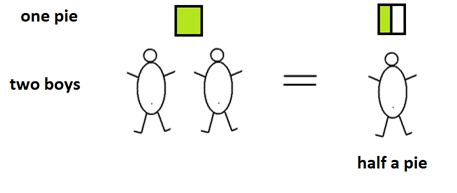
This brings us back in line with the start of these notes: half as part of a whole. In general, we call \(\frac{1}{n}\), the result of sharing \(1\) pie among \(n\) boys, “one \(n\)th.”
Now think about \(\frac{3}{5}\). In our sharing model this is the answer to sharing three pies equally among five boys:
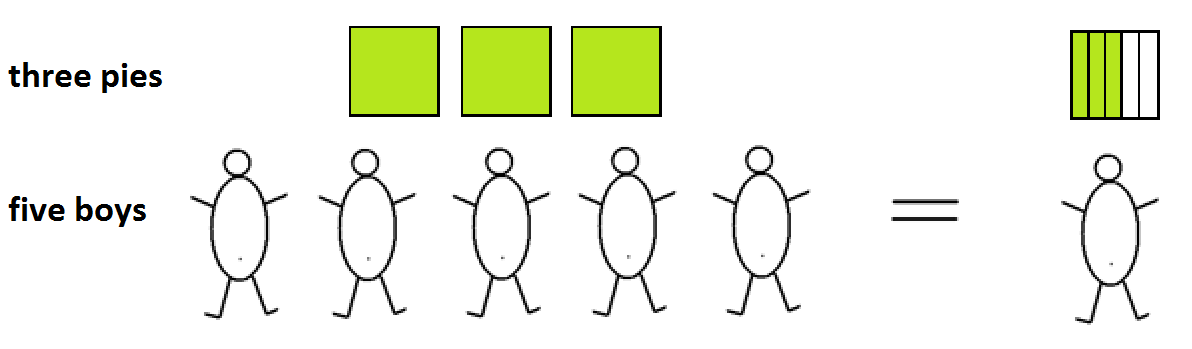
How might one physically accomplish this task?
One could divide each of the three pies into five equal pieces (fifths) and give one piece from each pie to each boy. This approach gives each boy three \(\frac{1}{5}\)s. For this reason, we call \(\frac{3}{5}\), “three fifths.”
Comment: In the number-line model, a fraction of the form \(\frac{1}{n}\) is set as the section length that results in dividing a unit line segment into \(n\) equal parts. Then \(\frac{a}{n}\) is set to be “\(a\) copies of \(\frac{1}{n}\).” That is, \(\frac{a}{n}\) is defined to be \(a\times \frac{1}{n}\) with repeated addition.
Some thinking questions about sharing:
Exercise:
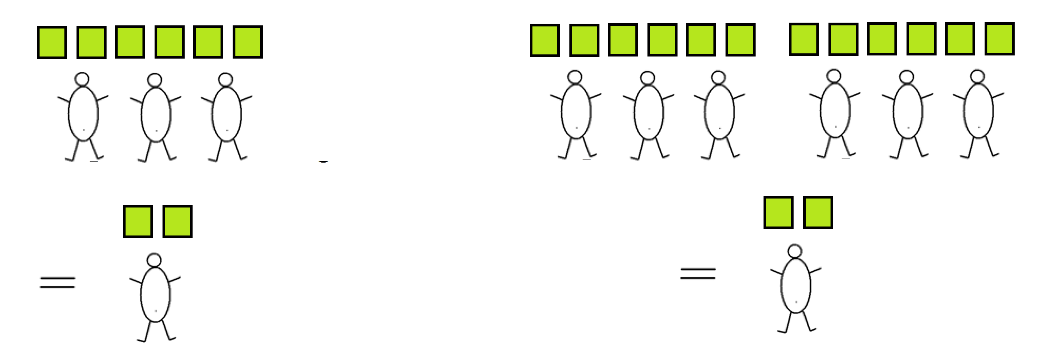
a) Here is the answer to a sharing problem:

This represents the amount of pie an individual boy receives if some number of pies is shared among some number of boys.
How many pies? _________
How many boys? _________
(Are answers here unique?)
b) Here is the answer to another sharing problem:
How many pies? _________
How many boys? _________
(Are answers here unique?)
Exercise: Leigh says that \(\frac{10}{13}\) is two times as big as \(\frac{5}{13}\). She argues:
In one room, ten pies are shared among thirteen boys.
In another room, five pies are shared among thirteen boys.
Each boy in the first room receives twice as much pie as each boy in the second room.
Do you agree?
Exercise: What does the sharing problem \(\frac{1}{1}\) represent? How much pie does an individual boy receive? What sharing problem does \(\frac{5}{1}\) represent and what is its result?
THE KEY FRACTION PROPERTY:
We have that \(\dfrac{a}{b}\) is an answer to a division problem:
\(\dfrac{a}{b}\) represents the amount of pie an individual boy receives when \(a\) pies are distributed among \(b\) boys.
What happens if we double the number of pies and double the number of boys? Nothing! The amount of pie per boy is still the same:
\(\dfrac{2a}{2b}=\dfrac{a}{b}\).
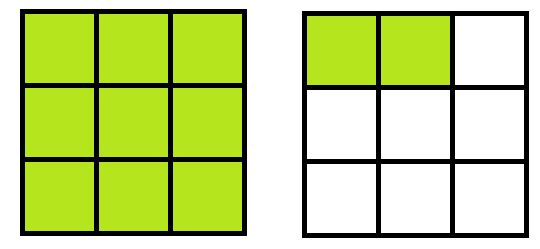
For example, this picture shows that \(\frac{6}{3}\) and \(\frac{12}{6}\) both give two pies to each boy:
And tripling the number of pies and tripling the number of boys also does not change the final amount of pie per boy, nor does quadrupling each number, or one-trillion-billion-tupling the numbers!
\(\dfrac{6}{3}=\dfrac{12}{6}=\dfrac{18}{9}=\ldots =\) two pies per boy.
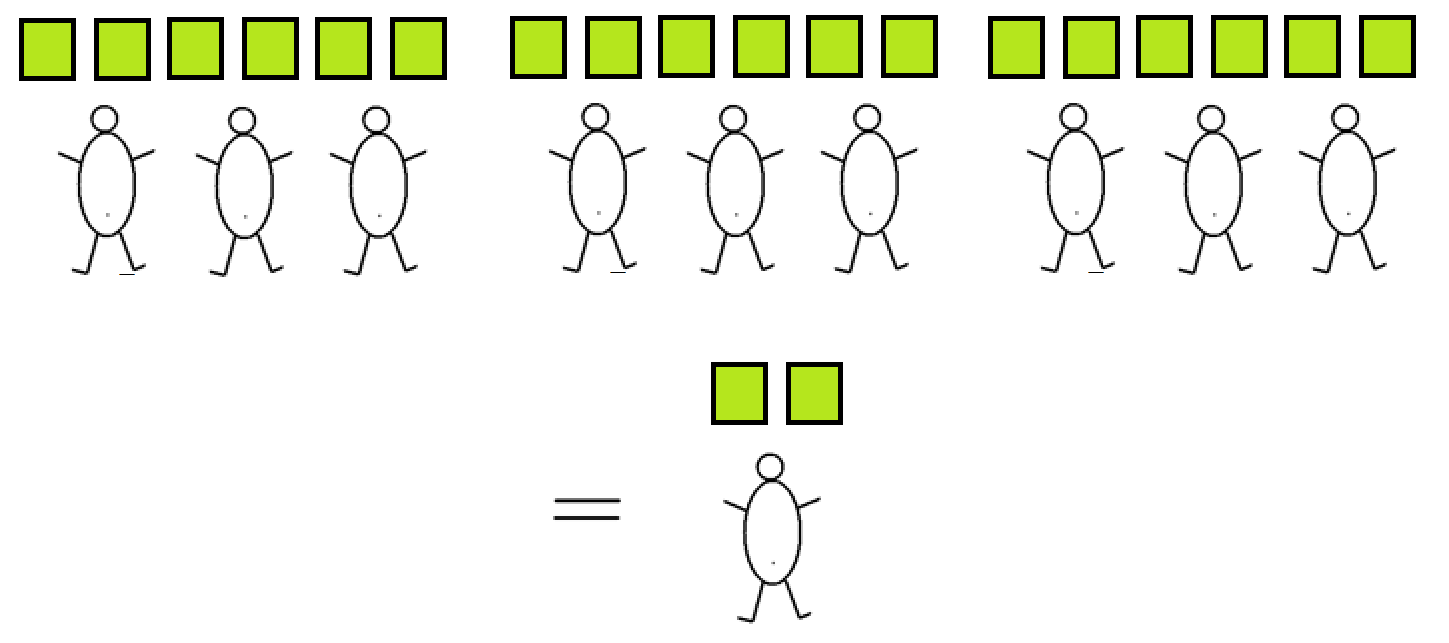
This leads us to want to believe a rule:
KEY FRACTION PROPERTY: \(\dfrac{xa}{xb}=\dfrac{a}{b}\) (at least for positive whole numbers).
For example,
\(\dfrac{3}{5}\) (sharing three pies among five boys)
yields the same result as
\(\dfrac{3\times2}{5\times2}=\dfrac{6}{10}\) (sharing six pies among ten boys),
and as
\(\dfrac{3\times100}{5\times100}=\dfrac{300}{500}\)(sharing \(300\) pies among \(500\) boys).
Going backwards:
\(\dfrac{20}{32}\) (sharing \(20\) pies among \(32\) boys)
is the same problem as:
\(\dfrac{5\times4}{8\times4}=\dfrac{5}{8}\) (sharing five pies among eight boys).
Comment: Most people say we have just “cancelled” a common factor of \(4\) from the numerator and the denominator and, in doing so, we have “simplified” the expression \(\frac{20}{32}\). (Admittedly, \(\frac{5}{8}\) is easier to conceptualize than \(\frac{20}{32}\).)
As another example \(\dfrac{280}{350}\) can certainly be made to look more manageable by noticing that there is a common factor of \(10\) in both the numerator and the denominator: \(\dfrac{280}{350}=\dfrac{28\times10}{35\times10}=\dfrac{28}{35}\). We can go further as \(28\) and \(35\) are both multiples of \(7\): \(\dfrac{28}{35}=\dfrac{4\times7}{5\times7}=\dfrac{4}{5}\). Thus, sharing \(280\) pies among \(350\) boys gives the same result as sharing just \(4\) pies among \(5\) boys: much easier to conceptualize! As \(4\) and \(5\) share no common factors, this is as far as we can go with this example – while staying with whole numbers. (Writing \(\frac{4}{5}=\frac{2}{2\frac{1}{2}}\) is mathematically fine!)
THE AREA APPROACH TO THE KEY FRACTION PROPERTY:
Here is a picture of some pie after sharing exercise:

We see it is a picture of \(\frac{2}{3}\), sharing two pies equally among three girls. (It’s time that girls got some pie too!)
But draw an extra cut in the picture, and we now see four-sixths, the result of sharing four pies among six girls.
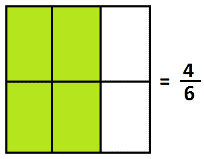
We haven’t changed the amount of pie, so \(\frac{4}{6}=\frac{2}{3}\). Or if we divide the amount of pie into three equal parts we see \(\frac{6}{9}=\frac{2}{3}\).
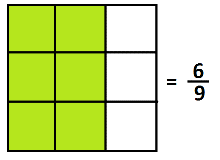
In general, dividing the picture of \(\frac{2}{3}\) into \(x\) equal parts we’ll see \(\dfrac{2x}{3x}=\dfrac{2}{3}\).
And of course there is nothing special about the amount \(\frac{2}{3}\) to begin with. In general, we have:
\(\dfrac{xa}{xb}=\dfrac{a}{b}\).
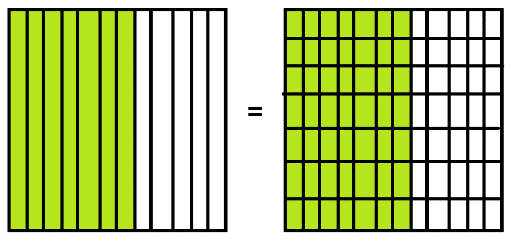
Comment: As an educator I personally find this a hard way to introduce the Key Fraction Property to students. The boys-and-pie model makes this rule seem natural and obvious. This area approach is subtle.
ADDING AND SUBTRACTING FRACTIONS:
If we think of fractions as amounts of pie that arise from sharing problems, then it makes sense, in that model, to add and subtract amounts of pie and get an answer that is the result of another sharing problem.
For example, here is a picture of \(\dfrac{2}{3}+\dfrac{2}{3}\).
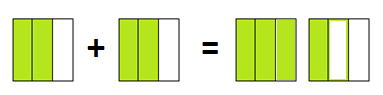
The result is four-thirds, the result of sharing four pies equally among three boys: \(\dfrac{2}{3}+\dfrac{2}{3}=\dfrac{4}{3}\).
In the same way we could draw a picture of \(\dfrac{2}{7}+\dfrac{3}{7}\) and see the answer \(\dfrac{5}{7}\). This really is as easy as saying “two sevenths plus three sevenths makes five sevenths,” just as two apples plus three apples makes five apples.
And we can add more than two fractions sharing a common denominator with the same ease, \(\dfrac{1}{10}+\dfrac{8}{10}+\dfrac{4}{10}=\dfrac{13}{10}\), and subtract fractions with a common denominator, \(\dfrac{6}{11}-\dfrac{2}{11}=\dfrac{4}{11}\).
The rub comes in trying to add or subtract fractions with different denominators.
Example: As a sharing problem, what is the result of \(\dfrac{2}{5}+\dfrac{1}{3}\)?
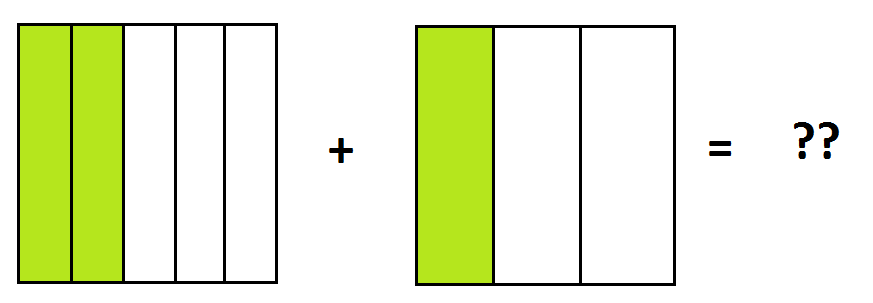
It is lovely that we can rewrite each of the expressions \(\dfrac{2}{5}\) and \(\dfrac{1}{3}\) in an infinitude of equivalent forms using the Key Fraction Property. By luck, we might find two expressions with a common denominator:
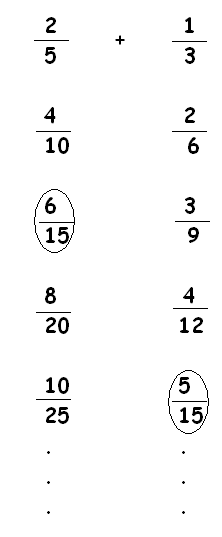
We do luck out and see that \(\dfrac{2}{5}+\dfrac{1}{3}\) is actually equivalent to the problem \(\dfrac{6}{15}+\dfrac{5}{15}\), which has answer \(\dfrac{11}{15}\). This work shows we could slice each of the two amounts of pie we have in our picture into fifteenths and all should then be clear. (And it is!)
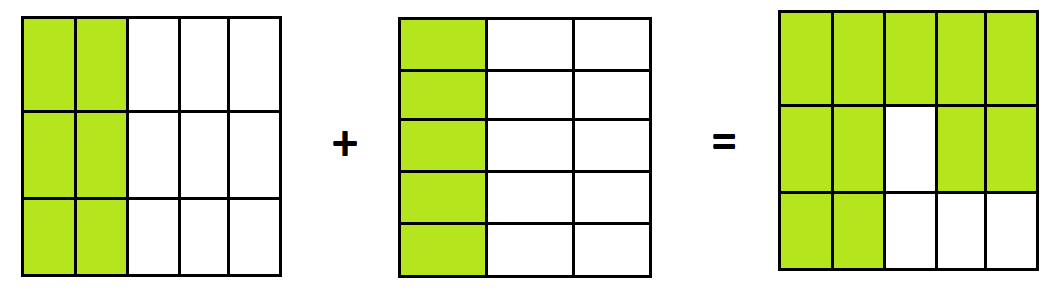
As another example:
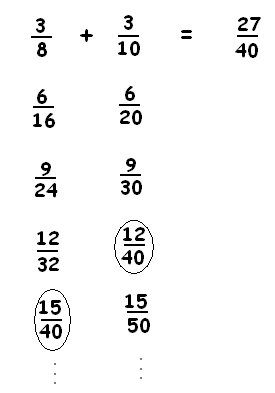
Comment: Of course there is an efficient way to find a “common denominator” of two fractions. Let students discover it.
Exercise: a) What is \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}\)? b) What is \(\dfrac{1}{2}-\dfrac{1}{4}-\dfrac{1}{8}-\dfrac{1}{16}\)?
Here’s a good question!
Exercise: Which is larger, \(\dfrac{5}{9}\) or \(\dfrac{6}{11}\)?
THE WORD “OF”:
In the world of fractions the word “of” is often used to imply sharing. But it is confusing.
For example, by “one-third of six” we mean “share six objects among three boys.” The result is two of those objects. So one-third of six is interpreted as \(\dfrac{6}{3}\). In general:
By “ \(\dfrac{1}{n}\) of \(a\)” we mean the sharing problem \(\dfrac{a}{n}\), the result of sharing the quantity \(a\) among \(n\) people.
This is the case even if \(a\) itself is a fraction!
Example: What is \(\dfrac{1}{3}\) of \(\dfrac{2}{5}\) ?
Answer: We are being asked to share the quantity \(\dfrac{2}{5}\) among three girls. In terms of pie, here is a picture of \(\dfrac{2}{5}\):

Here is the result, for each girl, of sharing it equally among the three of them. We see that this is a picture of \(\dfrac{2}{15}\).

Popular language has us read “\(\dfrac{2}{3}\) of \(6\)” as “two thirds of six,” that is, as two copies of one third of six. This is thus four objects out of a collection of six objects. In general:
By “\(\dfrac{x}{n}\) of \(a\)” we mean “\(x\) copies of \(\dfrac{1}{n}\) of \(a\).”
And, again, this is the case even if \(a\) itself is a fraction.
Example: What is \(\dfrac{2}{3}\) of \(\dfrac{2}{5}\)?
Answer: This time we want two copies of one-third of two-fifths.
Here’s \(\dfrac{2}{5}\).

Here’s one-third of \(\dfrac{2}{5}\).

Here’s two copies of one-third of \(\dfrac{2}{5}\). We see it is \(\dfrac{4}{15}\).

MULTIPLICATION OF FRACTIONS:
So far we have made sense of adding and subtracting fractions. Pinning down a sensible picture of multiplying fractions is surprisingly difficult.
And this, I think, illustrates why fractions are so hard: no model for how fractions are discussed in the early grades, in and of itself, gives a means or a context for multiplying fractions. In terms of portions of pie it makes perfect sense to add fractions. But what does it mean to multiply pie? Silly!

Now comes some flailing in many curriculums.
Look at the picture of “\(\dfrac{2}{3}\) of \(\dfrac{4}{5}\),” for example. We see the answer \(\dfrac{8}{15}\).

Notice that the left side of the rectangle is divided into three parts, with two of them shaded. And the top edge into five parts with four of them shaded. Switching from fractions being portions of area to portions of length, it looks like we have the fractions \(\dfrac{2}{3}\) and \(\dfrac{4}{5}\) in the picture.
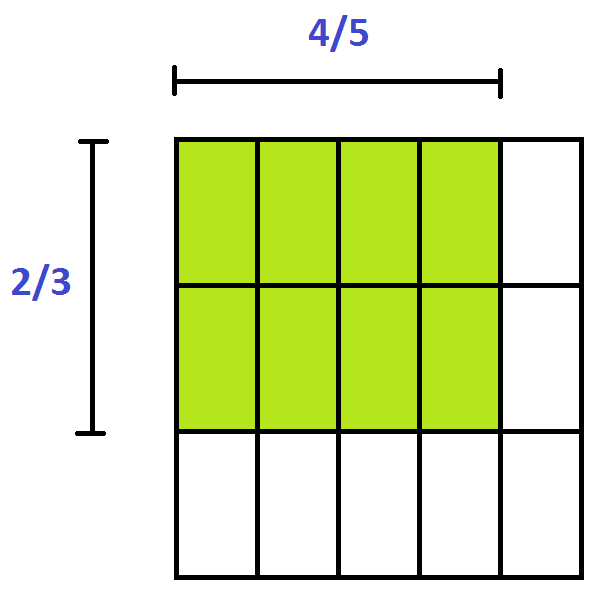
In fact, the whole picture looks like the area model for multiplication: we’ve shaded a rectangle with one side of length \(\dfrac{2}{3}\) and another of length \(\dfrac{4}{5}\). The area of this rectangle is the product of these two lengths. So let’s declare this picture to be the product of the two fractions! (Oh why not?) As the shaded region is fraction \(\dfrac{8}{15}\), we’ll declare this to be the answer to \(\dfrac{2}{3}\times\dfrac{4}{5}\).
Comment: Notice the changing roles of what a fraction is in this discussion: fractions are both being used as areas (portions of pie) and as lengths. This is actually confusing.
In general, many say:
Diagramming “\(\dfrac{a}{b}\) of \(\dfrac{c}{d}\)” (that is, \(a\) beeths of \(c\) deeths) gives a picture of pie divided into a total of \(bd\) pieces with \(ac\) of them shaded.
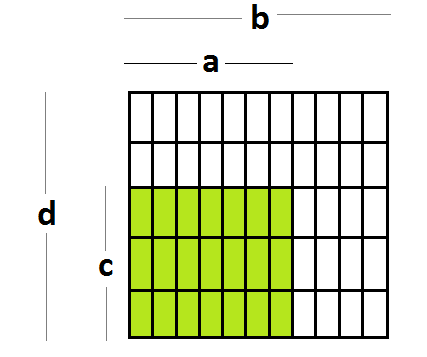
We see this as the product of \(\dfrac{a}{b}\) and \(\dfrac{c}{d}\) and so we define \(\dfrac{a}{b}\times\dfrac{c}{d}\) to be \(\dfrac{ac}{bd}\) .
That is, multiplication of fractions is simply defined to be a fraction of a fraction of a pie. The aphorism “of means multiply” is taken to heart in many curriculums.
Comment: All the above can indeed be properly justified in the proper context for fractions. The trouble is that the proper context needed is inappropriate for a student first-introduction to fractions! Educators are thus put in the awkward position of having to use models for fractions that don’t speak the whole truth about them, and switch back and forth between slightly inadequate models when developing a theory of fractions thereby making the subject feel confusing and arbitrary. A tough positon!
Please do look at Why Fractions are Hard for the full story.
Comment: We should discuss the division of fractions too. That is actually easier and is done in the essay.
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()


