By “two and a half pies” we mean two pies and another half a pie.

Even though we say the word “and” out loud, we tend to omit the plus sign in our mathematical writing. Thus \(2+\dfrac{1}{2}\) is usually written \(2\dfrac{1}{2}\) .

Sharing more pies than there are girls gives answers that can be expressed as mixed numbers. For example, if seven pies are shared among three girls, each girl will receive two whole pies and a third of a pie. We have \(\dfrac{7}{3}=2+\dfrac{1}{3}\).

As another example, consider \(\dfrac{23}{4}\). We can certainly give each girl five whole pies. That leaves three pies still be shared among the four girls. We see \(\dfrac{23}{4}=5\dfrac{3}{4}\).

Comment: Most people say: Four goes into \(23\) five times and leaves a remainder of \(3\), which is still be divided by four.

For a proper overview of mixed numbers see the Why Fractions are Hard essay.

THE ROLE OF THE AREA MODEL:

A common student mistake when working with mixed numbers is to say, for example, that \(5\dfrac{1}{3}\times4\dfrac{1}{2}\) is \(20\dfrac{1}{6}\). The area model shows students that there are more pieces than just \(5\times4\) and \(\dfrac{1}{3}\times\dfrac{1}{2}\) to contend with.

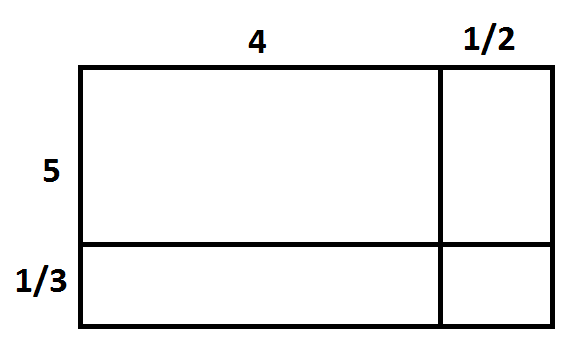
We have  \(5\dfrac{1}{3}\times4\dfrac{1}{2}=20+\dfrac{4}{3}+\dfrac{5}{2}+\dfrac{1}{6}=23+\dfrac{1}{3}+\dfrac{1}{2}+\dfrac{1}{6}=24\).

If the area model is part of student thinking from the get-go, this common error is easily attended to.

This work naturally extends to multiplying decimals.[See EXPLODING DOTS  for an overview of decimals. We have here an intersection point of two story-lines.] For example, here is a picture of \(4.2 \times 5.36\).

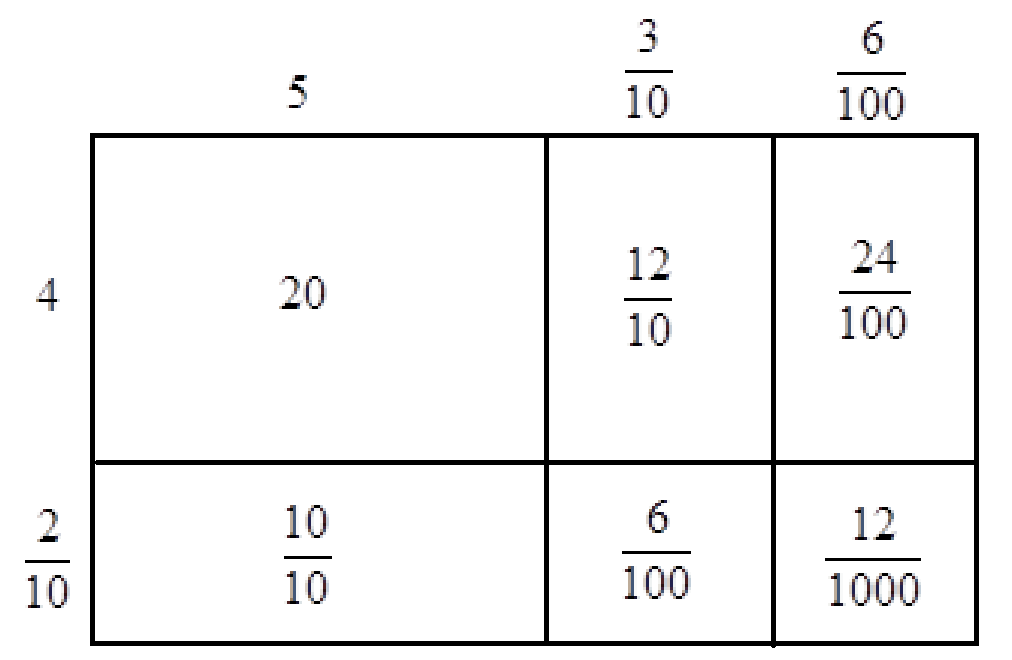
We see that the product is

\(20+\dfrac{22}{10}+\dfrac{30}{100}+\dfrac{12}{1000}=20+\left(2+\dfrac{2}{10}\right)+\dfrac{3}{10}+\left(\dfrac{1}{100}+\dfrac{2}{1000}\right)\)

\(=22+\dfrac{5}{10}+\dfrac{1}{100}+\dfrac{2}{1000}=22.512\).

Students can notice the lovely alignment tenths, hundredths, thousands along the diagonals.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources