In our base ten number system, the string of symbols “\(375\)” represents the number \(3\cdot10^{2}+7\cdot10+5\cdot1\). A polynomial is mathematical expression that looks like (or at least can be algebraically manipulated to look like) a number written base \(x\) for some unspecified quantity \(x\). For example, \(3x^{2}+7x+5\) is a polynomial in base \(x\) with integer coefficients (and if we are later told that \(x\) actually represents the number \(10\), then this expression corresponds to the number \(375\), to the number \(31\) if instead we are told \(x\) is \(2\), perhaps). The expression \(\pi w^{3}-5.2w^{2}+\frac{3}{\sqrt{6}}w+100\frac{3}{4}\) is a polynomial in the variable \(w\) with real coefficients.

A natural first appearance of polynomials comes through EXPLODING DOTS here with lesson 1.7 .

Multiplying two polynomials, say  \(x^{2} + 2x + 3\) and \(3x+1\), is just as easy, thanks to the area model, as multiplying two integers. (In fact easier, as one never needs to carry with polynomials!)

Notice the convenience of the diagonals: all like powers of \(x\) (or the powers of ten in ordinary arithmetic) match along them.

Of course, the area model is just a representation of Expanding Brackets: select one term from each set of parentheses and sum all possible products. As such, negative terms are permitted as entries in the diagrams.

For example, here is the product of \(x^{2}+2x-2\) and \(2x+3\).

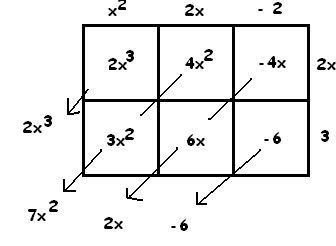
The answer \(2x^{3}+7x^{2}+2x-6\) appears.

Comment: This area model approach for polynomial work is often called the Galley Method.

EXERCISE: Compute the following products via the Galley Method.

a) \(\left(3x^{5}+2x^{4}-5x^{3}+4x^{2}-x+10\right)\left(x^{2}-3x+4\right)\)

b) \(\left(x^{3}-3x+2\right)\left(2x+5\right)\)

c) \(\left(x^{5}-x\right)\left(x^{4}-2x^{2}+1\right)\)

(For nice alignment of the diagonals, redo the second and third examples with zero rows and columns drawn in.)

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources