A nice feature of the area model for polynomial multiplication is that we can execute it backwards: if given the answer to a product of two polynomials and one of the polynomials in that product, it is easy to logically deduce what the second polynomial must be.

 

EXERCISE 1: Here is the table of a polynomial product given in the previous lesson. One of the polynomials in the product was \(2x+3\) and the  result of the product was \(2x^{3}+7x^{2}+2x-6\).   

The left-most diagonal has only one box, and so the top-left cell of the table must be \(2x^{3}\).

a) What must be the first term of the missing polynomial?

b) What must the remaining entry of the first column be?

c) Continue to fill in the table and to show that the missing polynomial is \(x^{2}+2x-2\).

 

The above example has computed \(\dfrac{2x^{3}+7x^{2}+2x-6}{2x+3}\) for us.

 

EXERCISE 2: Use the reverse area-model to compute \(\dfrac{2x^{2}+7x+6}{x+2}\).

(Solution is below.)

 

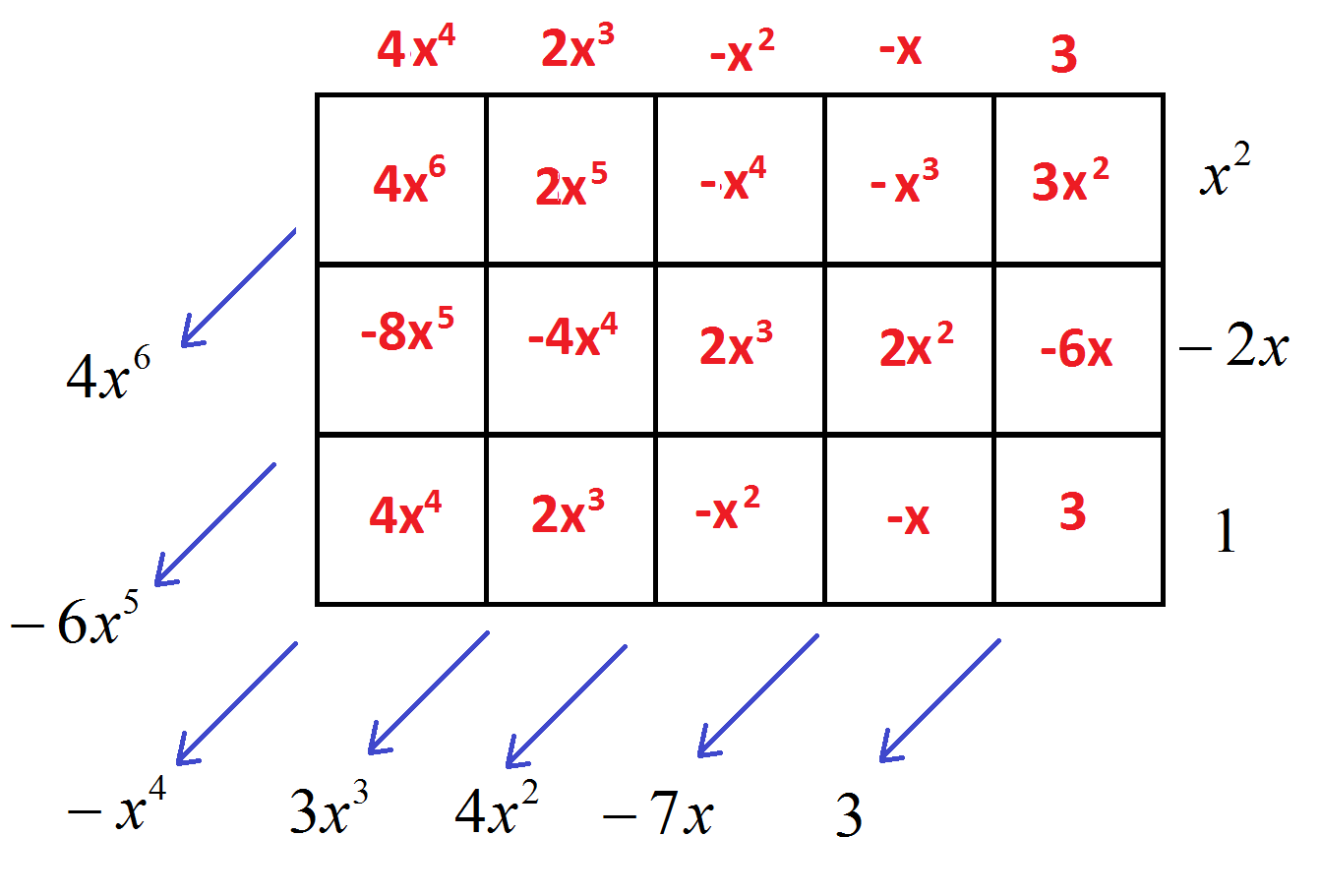
Consider the problem of computing \(\dfrac{4x^{6}-6x^{5}-x^{4}+3x^{3}+4x^{2}-7x+3}{x^{2}-2x+1}\).

 

The answer is the polynomial, which when multiplied by \(x^{2}-2x+1\), gives the product \(4x^{6}-6x^{5}-x^{4}+3x^{3}+4x^{2}-7x+3\). The table for this product has three rows (one for each of the terms \(x^{2}\), \(-2x\), and \(1\)) and has enough columns so as to have seven diagonals (one for each of the terms \(4x^{6}\), \(-6x^{5}\), \(-x^{4}\), \(3x^{3}\), \(4x^{2}\), \(-7x\), and \(3\)).  Some trial and error shows that table with five columns does the trick.

 

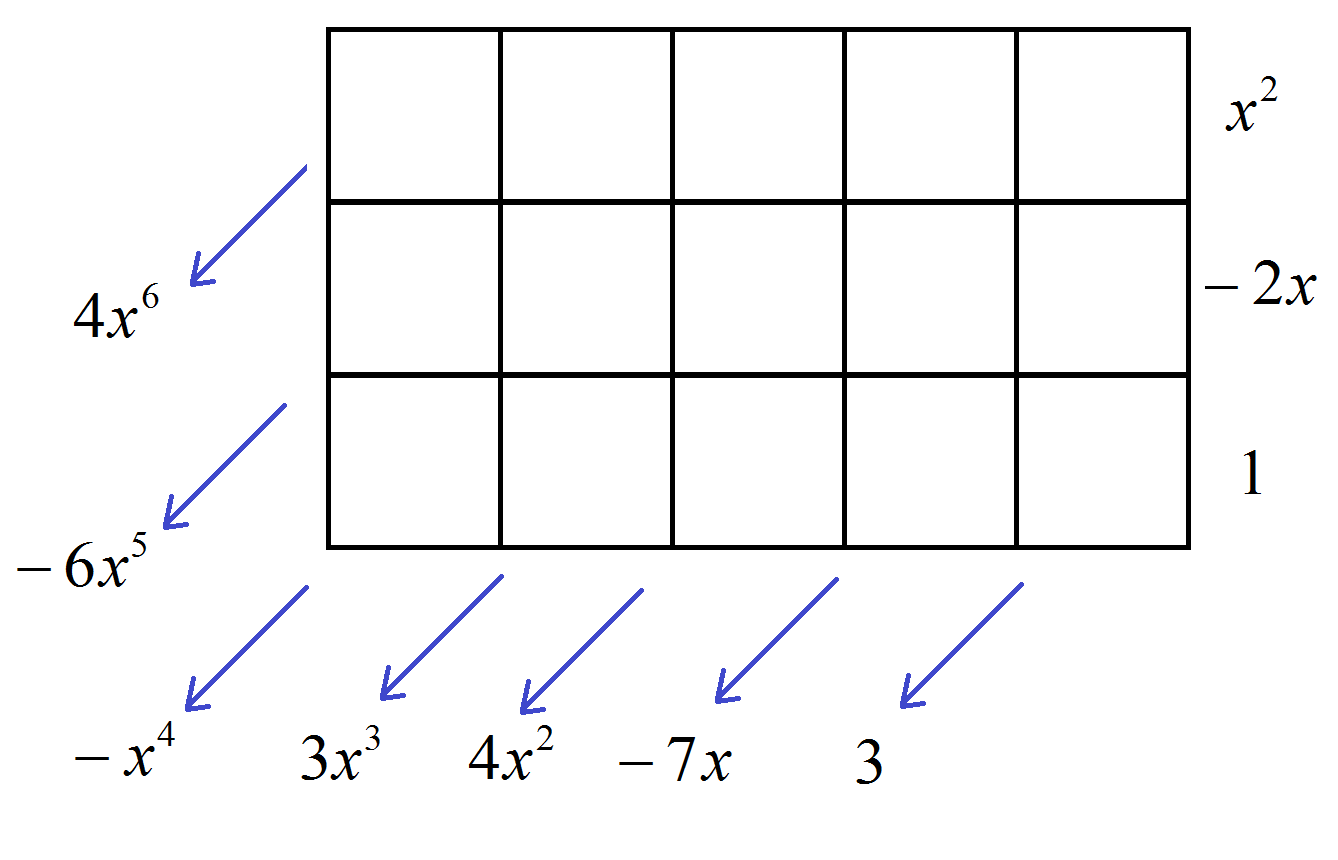
EXERCISE 3: Fill the cells of this table and compute . (Folk often start with the top-left cell of the table and work, column-wise, left to right. Must one start with that cell?)

 

One can deduce the number of columns needed without trial and error as follows. (Allow students to wonder about this and then, when appropriate, guide the following discussion.)

 

The answer to \(\dfrac{4x^{6}-6x^{5}-x^{4}+3x^{3}+4x^{2}-7x+3}{x^{2}-2x+1}\) is the polynomial, which when multiplied by \(x^{2}-2x+1\) gives a polynomial starting with \(4x^{6}\). So the answer must contain \(x^{4}\) as the highest power of \(x\). Thus our table will require five columns: one for the \(x^{4}\)  term, one for the \(x^{3}\) term, one for \(x^{2}\), one for \(x\), and one for a constant term.

 

 

EXERCISE 4: Compute again \(\dfrac{4x^{6}-6x^{5}-x^{4}+3x^{3}+4x^{2}-7x+3}{x^{2}-2x+1}\) , but this time use a table with three rows and EIGHT columns. Verify that misjudging the number of columns to the excess offers no cause for concern. (What happens if you guess too few columns?)

 

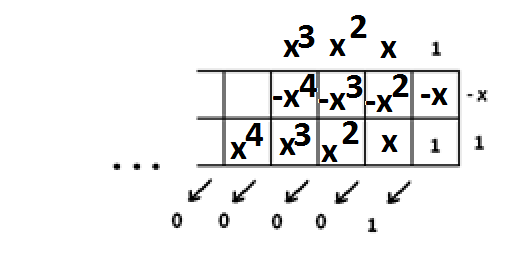
EXERCISE 5: Compute \(\dfrac{x^{5}+x^{3}+x^{2}-2x+2}{x^{3}-x+1}\). Is it helpful to keep track of zero coefficients?

 

EXERCISE 6: Solve the following division problems using the reverse area method.

a) \(\dfrac{x^{4}+2x^{3}+4x^{2}+6x+3}{x^{2}+3}\)

b) \(\dfrac{x^{6}-x^{5}+x^{4}-2x^{3}+6x^{2}-6x+4}{x^{4}-2x+4}\)

c) \(\dfrac{x^{8}-1}{x-1}\)

d) Is the number \(1028^{8}-1\) prime?  (People seem to forget that \(x\) can actually be a number in algebra class!)

 

EXERCISE 7: Algebra students are often taught to memorize the difference of two squares formula, \(x^{2}-a^{2}=\left(x-a\right)\left(x+a\right)\), and the difference of two cubes formula \(x^{3}-a^{3}=\left(x-a\right)\left(x^{2}+ax+a^{2}\right)\).

Compute \(\dfrac{x^{2}-a^{2}}{x-a}\)  and \(\dfrac{x^{3}-a^{3}}{x-a}\) via the reverse area method and so verify these formulas. (Care to find the general formula for \(\dfrac{x^{n}-a^{n}}{x-a}\)?)

 

EXERCISE 8:  This exercise makes you go WHOA!

a) Evaluate \(\dfrac{1}{1-x}\) via the reverse area method.

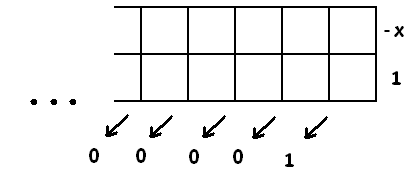
b) Evaluate \(\dfrac{1}{1+x}\) via the reverse area method.

c) Evaluate \(\dfrac{1}{1-x^{2}}\).

d) Compute \(\dfrac{1}{1-x-x^{2}}\)via the reverse area method. (What famous sequence of numbers do you see appear?)

 

Comment: The answers to these exercises show that, for example, IF \(1+x+x^{2}+x^{3}+\ldots\) has a meaningful value, then that meaningful value is sure to be \(\dfrac{1}{1-x}\). In calculus, one studies when such infinite sums have meaningful values. We see there, for example, that \(1+x+x^{2}+x^{3}+\ldots = \dfrac{1}{1-x}\) for \(-1<x<1\).

 

ANSWERS TO SELECT EXERCISES:

2. \(\dfrac{2x^2+7x+6}{x+2}=2x+3\)

3.  

 

5. Do think of this as \(\dfrac{x^{5}+0x^{4}+x^{3}+x^{2}-2x+2}{x^{3}+0x^{2}-x+1}\) to keep the diagonals aligned. The answer is \(x^{2}+2\).

6. a) \(x^{2}+2x+1\)  b) \(x^{2}-x+1\)  c) \(\dfrac{x^{8}-1}{x-1}=x^{7}+x^{6}+ \ldots +x+1\)

d) We just showed that \(x^{8}-1=\left(x-1\right) \times something\). Put \(x=1028\) to see that \(1028^{8}-1=1027 \times something\) and so is not prime.

8. a)  \(\dfrac{1}{1-x}=1+x+x^{2}+x^{3}+x^{4}+\ldots\)

b) \(\dfrac{1}{1+x}=1-x+x^{2}-x^{3}+x^{4}-\ldots\). (One can also just interchange \(-x\) for \(x\) in the answer to a).)

c) \(\dfrac{1}{1-x^{2}}=1+x^{2}+x^{4}+x^{6}+x^{8}+\ldots\).  (One can also just interchange \(x^{2}\) for \(x\) in the answer to a).)

d) \(\dfrac{1}{1-x-x^{2}}=1+x+2x^{2}+3x^{3}+5x^{4}+8x^{5}+13x^{6}+21x^{7}+\ldots\). We see the Fibonacci numbers.

 

Resources