Some school curricula teach students a rote method called synthetic division for dividing a polynomial by a linear term \(x-h\). It need not be mysterious as it is just the reverse area method in disguise. (In which case, why not just do the reverse area method?)

The approach of synthetic division was important in the day when all computations were done by hand and paper and pencil was precious. It is indeed a swift compactification of polynomial division (for the special case of polynomial division by a linear term). In this day and age, anyone needing a swift answer to such a division problem would simply type the task into Wolfram Alpha. So the process of synthetic division sits now as one of historical interest and no longer has a place in the classroom, especially if taught in a rote manner to be practiced in a rote manner.

Students can divide polynomials via the reverse area method with ease and understanding, and do more complex polynomial divisions than division by just linear terms, no sweat. But for the sake of completeness, here is discussion of synthetic division for historical interest.

Comment: It would be fine, and fun, carry out a class discussion like the outline below – but only as an aside for historical interest or as a “Why does this work?” puzzle to figure out.

Let’s take an abstract example.

EXAMPLE: Compute \(\left(ax^{3}+bx^{2}+cx+d\right)\div\left(x-h\right)\).

As an exercise, fill in the following table before reading on. Start with the top left corner and work from there.

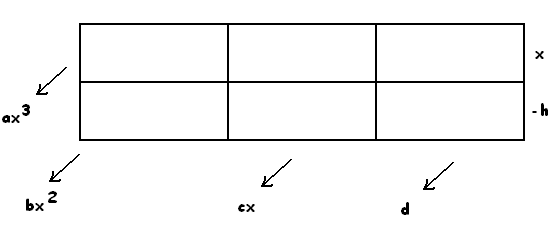
Here’s the result.

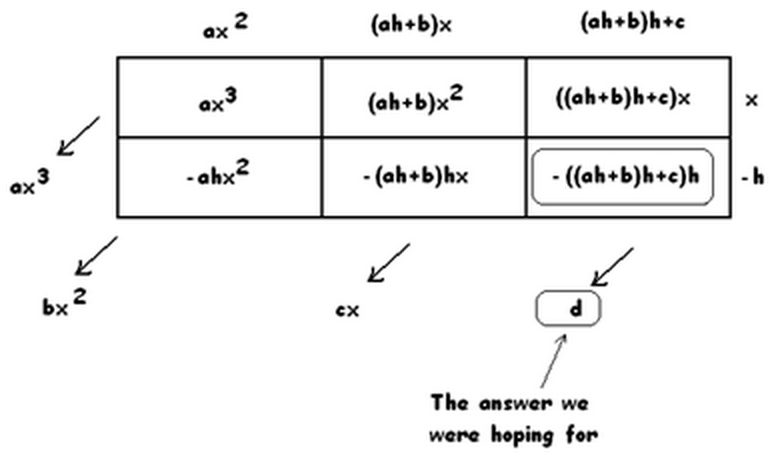
We see that

\(\dfrac{ax^{3}+bx^{2}+cx+d}{x-h}=ax^{2}+\left(ah+b\right)x +\left(\left(ah+b\right)h+c\right)+\dfrac{\left(\left(\left(ah+b\right)h+c\right)h+d\right)}{x-h}\).

Notice the coefficients that appear.

\(a\)

\(ah+b\)

\(\left(ah+b\right)h+c\)

\(\left(\left(ah+b\right)h+c\right)h+d\)

We start with \(a\), multiply it by \(h\) and add \(b\), multiply the result by \(h\) and add \(c\), multiply this next result by \(h\) and add \(d\).

Also observe that \(\left(\left(ah+b\right)h+c\right)h+d\) expands to \(ah^{3}+bh^{2}+ch+d\), which is the original polynomial evaluated at \(h\) (just as the Remainder Theorem says it should be).

Now let’s do a specific example:

EXAMPLE: Divide \(3x^{3}-7x^{2}+5x+11\)  by \(x-2\).

Here \(h=2\). The division process described above shows that we must take each coefficient of \(3x^{3}-7x^{2}+5x+11\) in turn, start with the \(3\), multiply by \(h\) and add the next coefficient, then multiply by \(h\) and add the next coefficient, and so on. Here goes.

\(3\)

\(3\times 2+\left(-7\right)=-1\)

\(\left(-1\right)\times 2+5=3\)

\(3\times 2 + 11=17\)

So \(\dfrac{3x^{3}-7x^{2}+5x+11}{x-2}=3x^{2}-x+3+\dfrac{17}{x-2}\) and we must have \(p\left(2\right)=17\).

It has become standard practice to perform this process using a table. In our example we write:

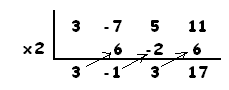
Can you see how to interpret this table?

EXERCISE: Compute the following and check your answers with either the reverse area method or with Wolfram Alpha.

a) \(\left(4x^{4}-2x^{3}+3x^2-7x+1\right)\div\left(x-3\right)\)

b) \(\left(2x^{5}-x^{3}+7x^2\right)\div\left(x+3\right)\)

Again … although the synthetic division process itself is nifty, it is specific only to division by linear terms. For understanding and clearness of mind it is actually better to engage in the reverse area method (or Exploding Dots method). One can apply it to all division problems with clarity and ease.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources