[This material appears in Section 2 of the full course on Quadratics.]

Let’s now explain the quadatus method for solving quadratic equations. We’ll start with quadratic equations that are overtly connected to squares and tweak our sophistication from there.

 

LEVEL 0 QUADRATIC EQUATIONS

Just a few examples should do it.

 

EXAMPLE: Solve \(x^{2}=100\).

Answer: Easy. \(x=10\) or \(x=-10\).

The only possible difficulty here is to remember that, in algebra, positive quantities have two square roots. (See the comment in lesson 2.1.)

 

EXAMPLE: Solve \(w^{2}=36\).

Answer: Easy. \(w=6\) or \(w=-6\).

 

EXAMPLE: Solve \(x^{2}=17\).

Answer: Okay, not as pretty but just as easy: \(x=\sqrt{17}\) or \(x= -\sqrt{17}\).

 

EXAMPLE: Solve \(x^{2}=0\).

Answer: Zero is the only number with just one square root. We have \( x=0\) .

 

 

EXERCISE 1: Solve:

a) \(x^{2}=121\).

b) \(p^{2} = 40\).

c) \(y^{2} + 5 = 14\).

d) \( 2x^{2} = 50\).

e) \(x^{2}=-6\).

 

EXERCISE 2: Leela was asked to solve \(x^{2}=1\). She wrote: \(x=\sqrt 1\) or \(x=-\sqrt 1 \). What do you think of her answer?

 

LEVEL 1 QUADRATIC EQUATIONS

Up a slight notch in trickiness.

 

EXAMPLE: Solve \((x+3)^{2}=100\).

Answer: This problem is saying “Something squared is \(100\). ”  So the something must be \(10\) or \(-10\). That is:

\(x+3=10\)   or   \(x+3=-10\)

yielding

\(x=7\)    or   \(x=-13\).

 

EXAMPLE: Solve \((y-4)^{2} = 25\).

Answer: We have:

\(y-4=5\)    or    \(y-4=-5\)

yielding

\(y=9\)    or   \(y=-1\).

 

 

WARNING!  Many like to answer these questions using the \(\pm\) symbol. But there is a potential danger as it is tempting to write the following:

\((y-4)^{2}=25\)

\(y-4=\pm 5\)

\(y=\pm 9\)

Do you see the danger? This is why I personally prefer to write things out and make sure I am thinking through everything carefully.

\(y-4=5\)    or    \(y-4 = -5\)

\(y=9\)    or   \(y=-1\)

This is now very clear and very correct. It never hurts to take an extra two seconds for the sake of clarity.

 

EXAMPLE: Solve \(4(p+2)^{2}-16=0\).

Answer: Add 16

\(4(p+2)^{2}=16\).

Divide though by 4

\((p+2)^2=4\)

to see

\(p+2=2\)   or   \(p+2=-2\).

This yields

\(p=0\)    or    \(p=-4\).

 

EXAMPLE: Solve \((x+7)^{2}+9=0\).

Answer: We have \((x+7)^{2}=-9\).   In the system of real numbers, it is impossible for a quantity squared to be negative. This equation has no solution.  (But if you like to work with complex numbers …)

 

EXAMPLE: Solve \((x-1)^{2}=5\).

Answer: We have

\(x-1=\sqrt 5\)    or    \(x-1=-\sqrt 5\)

so

\(x=1+\sqrt 5\)    or   \(x=1-\sqrt 5\).

 

EXAMPLE: Solve \((x+3)^{2}=49\).

Answer: We have

\(x+3=7\)    or    \(x+3=-7\)

yielding

\(x=4\)    or    \(x=-10\).

 

EXERCISE 3: Solve.

a) \((x-1)^{2}=64\)

b) \((p-3)^{2}=16\)

c) \((y+1)^{2}-2=23\)

d) \(3(x-900)^{2}=300\)

e) \((x-\sqrt 2)^{2}=5\)

EXERCISE 4:

a) How many solutions does \((x+7)^{2}=0\) possess? What are they?

b) How many solutions does \((x+7)^{2}=-2\) have? What are they?

 

LEVEL 2 QUADRATICS

Here’s a conceptual leap!

 

EXAMPLE: Solve \(x^{2} + 6x+9=49\).

Answer:  If one is extremely clever one might realize that this is a repeat of the example \(\left(x+3\right)^{2}=49\) we just did: the quantity \(x^{2} + 6x+9=49\) happens to equal \((x+3)^{2}\).

To check this, work out \((x+3) \times (x+3)\) as the area of a square divided into four pieces to see it is \(x^{2} + 6x+9=49\) in disguise.

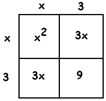
So the challenge

Solve \(x^{2} + 6x+9=49\)

is indeed the previous example

Solve \((x+3)^{2} =49\)

in disguise. We have:

\(x+3=7\)    or    \(x+3=-7\)

\(x=4\)    or    \(x=-10\).

 

The challenge in level 2 is to recognize more complicated expressions as easy level 1 problems in disguise.

We’ll do this next.

Resources