Many students are taught to solve quadratics by memorizing the famous quadratic formula. There is no need: The box method with the symmetry of the square will never let you down!  The reason I say this is because the box method really is the quadratic formula that everyone does, just made natural and bare. (In fact, my students use the box method to derive the quadratic formula just as an incidental exercise.)

 

Those who use the quadratic formula are taught to bring all the terms to one side so that it is an equation with zero on one side. We can do this too if we want (but the box method does not require it!)

\(ax^{2}+bx+c=0\)

If we use the box method on this, we multiply through by \(a\) to make the first term a perfect square and through by \(4\) to avoid fractions. This gives:

\(4a^{2}x^{2}+4abx+4ac=0\).

Now apply the box method:

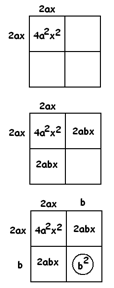
The box shows that we need the number \(b^{2}\), not \(4ac\), in the equation \(4a^{2}x^{2}+4abx+4ac=0\). Let’s subtract \(4ac\),

\(4a^{2}x^{2}+4abx=-4ac\)

and add \(b^{2}\)

\(4a^{2}x^{2}+4abx+b^{2}=b^{2}-4ac\).

Now looking at the box we are set to go.

\(4a^{2}x^{2}+4abx+b^{2}=b^{2}-4ac\)

\((2ax+b)^{2}=b^{2}-4ac\)

\(2ax+b=\sqrt{b^{2}-4ac}\)  or  \(-\sqrt{b^{2}-4ac}\).

Now add \(-b\) throughout

\(2ax=-b+\sqrt{b^{2}-4ac}\)  or  \(-b-\sqrt{b^{2}-4ac}\).

And divide through by \(2a\)

\(x=\frac{-b+\sqrt{b^{2}-4ac}}{2a}\)  or   \(x=\frac{-b-\sqrt{b^{2}-4ac}}{2a}\).

This statement can be combined into a single expression:  \(x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\).

 

THE QUADRATIC FORMULA: If \(ax^{2}+bx+c=0\), then  \(x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\).

 

COMMENT: Many curricula have students solve all quadratic equations by applying this memorized formula. This has the advantage of being quick. I will never stop a student from following this route too, but I personally prefer following a method I feel I understand and can just do without any memorization. It stays with me in the long run and makes sense. There is no need to do math fast!

 

FOR THOSE THAT INSIST ON KNOWING THE QUADRATIC FORMULA

The box method shows that the general quadratic equation \(ax^{2}+bx+c=0\) has general solution: \(x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\). Many curricula have students not only memorise this formula, but also study different features of the formula, and give parts of it names.

 

The quantity under the square root sign, \(b^{2}-4ac\), is called the discriminant of the quadratic. Folk like to give this quantity a name because its sign determines the types of solutions one obtains:

If \(b^{2}-4ac\)   is negative, then the quadratic has no real solutions. (One cannot compute the square root of a negative value.)

If \(b^{2}-4ac\)   equals 0, then the quadratic has precisely one solution. (Zero is the only number with precisely one square root.)

If \(b^{2}-4ac\)   is positive, then the quadratic has two real solutions. (There are two square roots to a positive quantity.)

 For example, without any effort we can see:

\(2w^{2}-3w+4=0\) has no solutions because is \(b^{2}-4ac =3^{2}-4 \cdot 2 \cdot 4=-23\)  is negative.

\(x^{2}-4x+4=0\) has precisely one solution because \(b^{2}-4ac =16-16=0\).

\(3y^{2}-y-1\) has precisely two solutions because \(b^{2}-4ac =1+12=13\) is positive.

 

People also note that the two solutions to a quadratic can be written:

\(x=-\frac {b}{2a} + \frac {\sqrt{b^{2}-4ac}} {2a} \)  and  \(x=-\frac {b}{2a} – \frac {\sqrt{b^{2}-4ac}}{2a}\).

 This shows that the two solutions lie at symmetrical positions about the value:

\(x=-\frac {b} {2a}\).

Some folk consider this important to hold in mind.

 

Comment: See Part 4 of the Quadratics Course as to why none of this is necessary.

 

SHOULD ONE MEMORISE THE QUADRATIC FORMULA?

If speed matters to you … maybe.

If a curriculum  insists that you and your students know it and that you must use the word “discriminant,”  then yes, I suppose.

But if understanding has a higher priority in your mind, then the box method will not let you down.

To solve \(ax^{2}+bx+c=0\) just multiply through by \(a\) to make \(ax^{2}\) a square and also multiply through by \(4\)  to avoid fractions. Then let the box guide you!

Resources