Suppose \(100\) people walk down a garden path that leads to a fork. Those who turn left go to house A, those who turn right to house B. Assume that there is a \(50\%\) chance that a person will turn one way over the other.

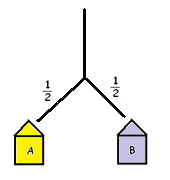
In this set-up we’d expect, essentially, \(50\) people to end up at house A and \(50\) people at house B.  The following diagram of one-hundred dots (for \(100\) people) depicts this outcome.

 

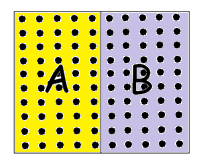
The number \(100\) here is immaterial. The point is that if a square is used to denote the entire population of people walking down the path, then half the area of the square, half the people, is designated by result A and the second half of the square with result B.

 

Playing with examples like these is fun!

 

EXAMPLE: Folk walk down the following system of paths. Use the square model to compute the fraction of people that end up at house A, at house B, and at house C. (Assume that at each fork equal numbers of people choose each direction.)

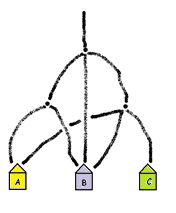
 Answer: At the first fork, a third of the people turn left, a third go straight, and a third turn right.

Of those that turn left, half go to house A and half go to house B.

All those who go straight, go to house B.

Of those who turn right, a third go to A, a third to B, and a third to C.

We have the picture:

We see now that the proportion of people that end up in house A is given as half of a third, that’s \(\dfrac{1}{6}\), plus a third of a third, that’s \(\dfrac{1}{9}\).  This proportion is \(\dfrac{1}{6}+\dfrac{1}{9}=\dfrac{5}{18}\).

The proportion of people that end up in house B is \(\dfrac{1}{6}+\dfrac{1}{3}+\dfrac{1}{9}=\dfrac{11}{18}\).

The proportion of people that end up in house C is \(\dfrac{1}{9}=\dfrac{2}{18}\).

Question: Does it make sense that these three answers add to \(1\)?

 

EXERCISE: People walk down the following system of paths. Use the square model to compute the fraction of people that end up at each house. (Again assume that at each fork equal numbers of people choose each direction.)

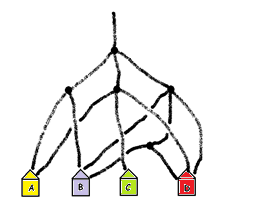
(Just so you have it, the answers are \(\dfrac{5}{18}\), \(\dfrac{6}{18}\), \(\dfrac{2}{18}\), and \(\dfrac{5}{18}\).)

 

Of course, in sending people down these garden paths, we’re really looking at the outcome of performing a probability experiment a large number of times.

 

EXAMPLE: I roll a die and then toss a coin. What are the chances of seeing an even number followed by a head?

Answer: Think of this as a path-walking problem with two houses labeled “WANT” and “DON’T WANT.” The forks in the road represent the options that can occur (each, with \(50\%\) chance of occurring).

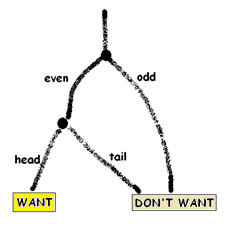
This leads to the square model diagram:

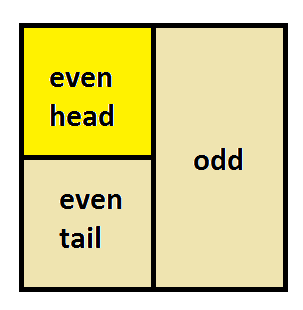
We see that the desired outcome represents one quarter (half of a half) of the square. Thus \(p(\) Even and then Head\( )=\dfrac{1}{4}\).

 

EXAMPLE: I toss a quarter, then I toss a dime, and then I roll a die. What are the chances of receiving a head, then a head, and then a \(5\) or a \(6\)?

Answer: Here’s the garden path.

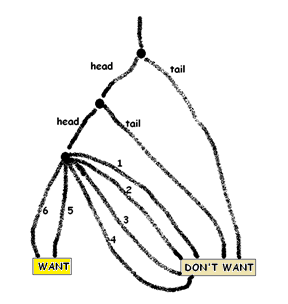
This gives the square model:

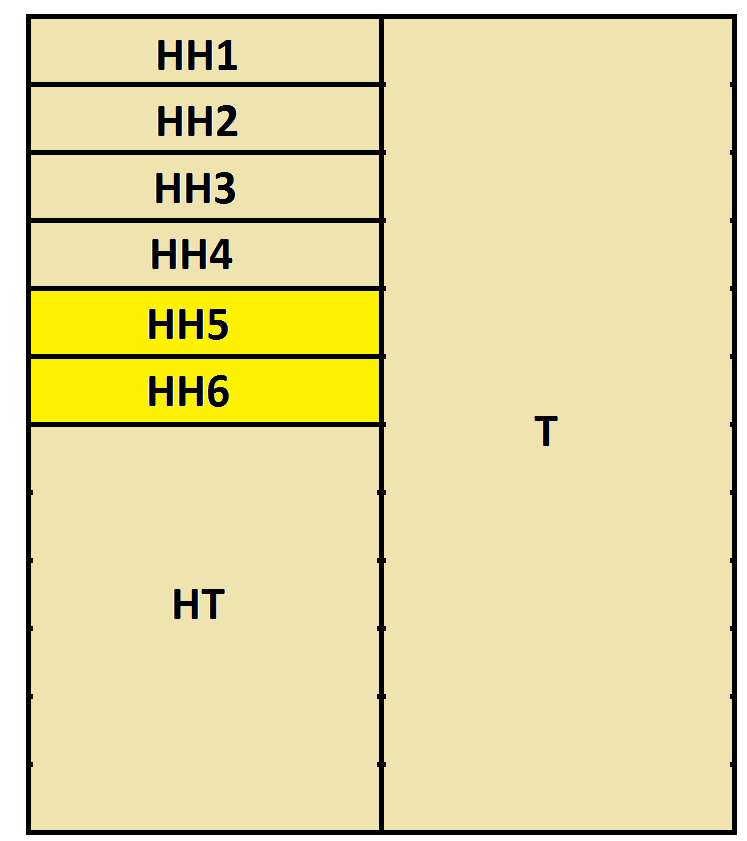
We have

\(p(\) Head and then Head and then \(\{5 or 6\} ) = \dfrac{2}{6}\) of \(\dfrac{1}{2}\) of \(\dfrac{1}{2}\) the square

\(=\dfrac{2}{6}\times\dfrac{1}{2}\times\dfrac{1}{2}=\dfrac{1}{12}\).

 

Each of the fractions appearing in the product of the answer is a fraction corresponding to the probability of a desired outcome in one of the individual actions: \(\dfrac{2}{6}\)  is the probability of rolling a five or a six with the die,  \(\dfrac{1}{2}\) is the probability of flipping a head with the dime, and \(\dfrac{1}{2}\)  is the probability of flipping a head with the quarter.

 

The area model shows that the final answer is a fraction given by a fraction of a fraction of a fraction of the entire square, that is, the product of these fractions.

In general:

 

MULTIPLICATION PRINCIPLE IN PROBABILITY THEORY: Special Version

If one performs one action and hopes to receive outcome \(A\) and then performs a second, completely unrelated, action and hopes to receive outcome \(B\), then the probability of seeing \(A\) and then \(B\) is the product of the individual probabilities. That is

\(p( A\) and then \(B ) = p(A) \times p(B)\)  for independent actions.

 

The garden path model shows this:  \(p ( A\) and then \(B )\) is seen as a fraction of a fraction of the area of a square.

 

Resources