The multiplication principle stated in the previous lesson relies on actions being independent, that the outcome of one action can in no way affect the outcome of the other action. Yet we often teach students to use this principle any time the word “and” appears in a probability problem, even if the events involved are NOT independent. I often hear the aphorism “And means multiply” bandied about in a care-free manner.

So, does “and” always correspond to arithmetic of multiplication?

Consider the following two problems:

EXAMPLE 1: (A “with replacement” problem.) A bag contains two red balls and three yellow balls. I pull out a ball at random, note its color, put the ball back, and pull out a second ball at random. What are the chances I see two red balls?

EXAMPLE 2: (A “without replacement” problem.) A bag contains two red balls and three yellow balls. I pull out a ball at random, note its color, and put it aside. I then pull out a second ball at random from the four balls that remain in the bag. What are the chances I see two red balls?

The two actions in Example 1 are certainly independent (in no way does the outcome of pulling out a ball the first time affect the outcome of pulling out a ball a second time), and so by the multiplication principle from the previous lesson we do have

\(p(\) RED and RED \( )= \dfrac{2}{5}\times \dfrac{2}{5} = \dfrac{4}{25}\).

But the two events in the Example 2 are not independent:  the result of the first action affects the possible results of the second. (The probability of choosing a red second ball is either \(\dfrac{1}{4}\) or \(\dfrac{2}{4}\) depending on the outcome of the first action.) If we blindly follow the aphorism  “And means multiply,” then matters are confusing.

Is  \(p(\) RED and RED \(= \dfrac{2}{5}\times \dfrac{1}{4} = \dfrac{2}{20}\) or is \(p(\) RED and RED \(= \dfrac{2}{5}\times \dfrac{2}{4} = \dfrac{4}{20}\)?

A good way out of these pickles is to draw a garden path for the problem. Here’s a diagram for Example 2. (Notice there is one path for each ball in the bag.)

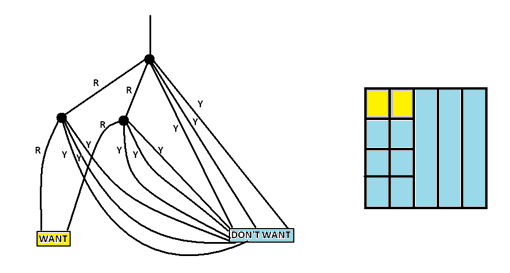
We see \(p(\) RED and RED \( )= \dfrac{2}{5}\times \dfrac{1}{4} = \dfrac{2}{20}\). Confusion cleared and we’re done!

Garden paths will not let you down. There really is no need for anything more!

But for the purposes of this topic, we want to ask: Was a multiplication principle at play here? 

Look again at the garden path we drew for this example. In a class conversation someone will invariably comment that we could have drawn a simplified version of the garden path model.  GREAT!  (Let students suggest these ideas.)

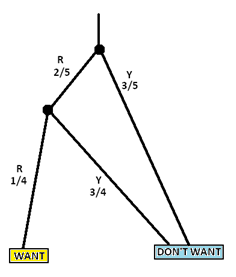
In this diagram, directions from a fork are no longer given equal weight: the probabilities of making a particular turn match the probabilities of the outcomes from the event the fork represents.

The area model now shows very directly a product of fractions:

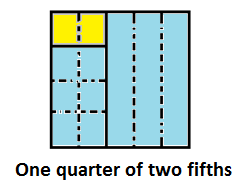
We have multiplication:

\(p(\) RED and RED\()= \dfrac{2}{5}\times \dfrac{1}{4} = \dfrac{2}{20}\).

So it seems that “and” does correspond to the action of multiplication from this perspective.

For those who like general statements of principles (one can always just “nut things out” with garden paths), here it is:

MULTIPLICATION PRINCIPLE IN PROBABILITY THEORY: General Version

Suppose one performs one task and hopes to get outcome \(A\), and then performs a second task and hopes to get outcome \(B\). To work out the probability of seeing \(A\) and then \(B\), first work out:

\( p(A)\), the probability of seeing \(A\).

\(p(B\vert  A)\), the probability of seeing \(B\) under the assumption you have just seen\(A\).

Then:

\(p( A\) and then \(B) = p(A) \times p(B \vert A)\).

NOTE: If the two events are independent, that is, the outcome of the first task in no way affects the outcome of the second, then \(p(B \vert A) = p(B)\). (The chances of seeing \(B\) are irrelevant to whether or not we’ve just seen \(A\).)  In this case,

\(p( A\) and then \(B) = p(A) \times p(B )\).

and we have the multiplication principle we first described.

Comment: Garden paths are really much more fun!

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources