See how Goldfish & Robin and friends, “Math on the Path,” explain these ideas too: Kids Explain Math For Kids. And here is a video from that team in Spanish. 

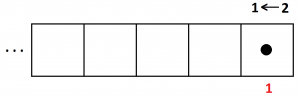
Okay. Let’s go back to the \(1 \leftarrow 2\) machine and make sense of what curious device is doing. Recall that it follows the rule

Whenever there are two dots in any one box they “explode,” that is, disappear, and are replaced by one dot, one place to their left.

And this machine is set up so that dots in the rightmost box are always worth one.

With an explosion, two dots in the rightmost box are equivalent to one dot in the next box to the left. And since each dot in the rightmost box is worth \(1\), each dot one place over must be worth two ones, that is, \(2\).

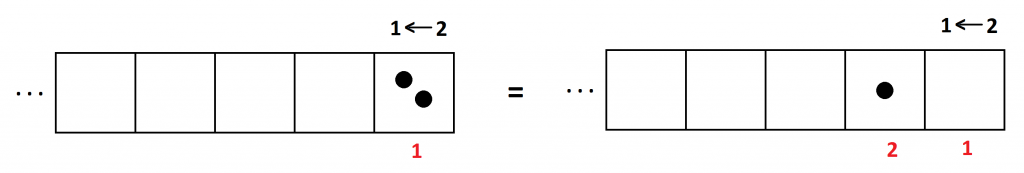
And two dots in this second box is equivalent to one dot one place to the left. Such a dot must be worth two \(2\)s, that is, worth \(4\).

And two fours makes \(8\) for the value of a dot the next box over.

Here’s a question to mull on if you like. Remember my solutions to all questions appear in the final section of this chapter.

1. The value of a dot one further place to the left is \(16\). Can you see why? What are the values of dots in the next few boxes even further to the left?

We saw earlier that the code for thirteen in a \(1 \leftarrow 2\) machine is \(1101\). Now we can see that this is absolutely correct: one \(8\) and one \(4\) and no \(2\)s and one \(1\) does indeed make thirteen.

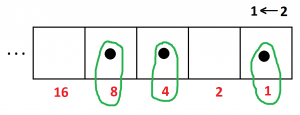
We also asked what number has code \(10110\) in a \(1 \leftarrow 2\) machine. We now readily see that the answer is \(16+4+2=22\).

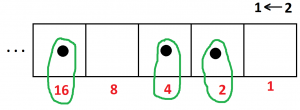
Can you see that the \(1 \leftarrow 2\) code for thirty is \(11110\)?

2. What number has \(1 \leftarrow 2\) code \(100101\)?

3. What is the \(1 \leftarrow 2\) code for the number two hundred?

People call the \(1 \leftarrow 2\) codes for numbers the binary representations of numbers (with the prefix bi- meaning “two). They are also called base two representations.  One only ever uses the two symbols \(0\) and \(1\) when writing numbers in binary.

Computers are built on electrical switches that are either on or off. So it is very natural in computer science to encode all arithmetic in a code that uses only two symbols: say \(1\) for “on” and \(0\) for “off.” Thus base two, binary, is the right base to use in computer science.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources