Exploding Dots
3.2 Addition
Lesson materials located below the video overview.
See how Goldfish & Robin |Where Young Minds Collide” push the ideas of this lesson even further: Kids Explain Math For Kids. And here is a lovely video from the Spanish team of youngsters (in Spanish) explaining addition too (with a final section trying to teach me Spanish!)
Here’s an addition problem: Compute \(251+124\).
Such a problem is usually set up this way.
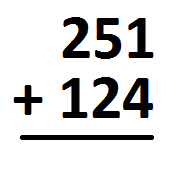
This addition problem is easy to compute: \(2+1\) is \(3\), \(5+2\) is \(7\), and \(1+4\) is \(7\). The answer \(375\) appears.
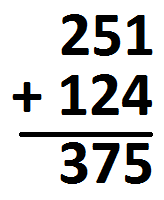
But did you notice something curious just then? I worked from left to right just as I was taught to read. This is usually opposite to what most people are taught to do in a mathematics class: go right to left. Even though we went the opposite direction, our answer \(375\) is correct. (Check: Do you get the same answer if we work the other way?)
So why are we taught to work right to left in mathematics classes?
Many people suggest that the problem we just did is “too nice.” We should do a more awkward addition problem, one like \(358+287\).
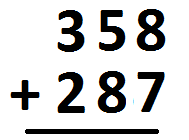
Okay. Let’s do it!
If we go from left to right again we get \(3+2\) is \(5\); \(5+8\) is \(13\); and \(8+7\) is \(15\). The answer “five-hundred thirteenty fifteen” appears. (Remember, “ty” is short for ten.)
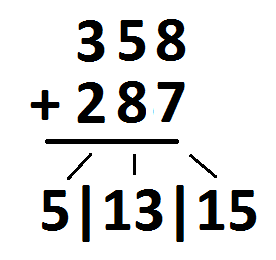
And this answer is absolutely mathematically correct! You can see it is in a \(1 \leftarrow 10\) machine. Here are \(358\) and \(287\).
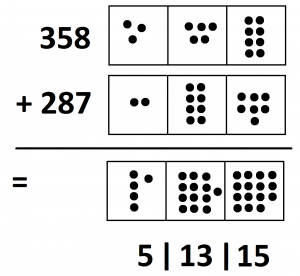
Adding \(3\) hundreds and \(2\) hundreds really does give \(5\) hundreds.
Adding \(5\) tens and \(8\) tens really does give \(13\) tens.
Adding \(8\) ones and \(7\) ones really does give \(15\) ones.
“Five-hundred thirteenty fifteen” is absolutely correct as an answer – and I even said it correctly. We really do have 5 hundreds, 13 tens, and 15 ones. There is nothing mathematically wrong with this answer. It just sounds weird. Society prefers us not to say numbers this way.
So the question is now:
Can we fix up this answer for society’s sake – not mathematics’ sake – just for society’s sake?
The answer is yes! We can do some explosions. (This is a \(1 \leftarrow 10\) machine, after all.)
Let’s explode ten dots in the middle box and replace them with one dot, one place to the left.
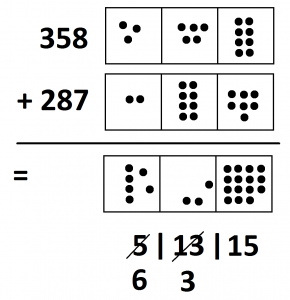
The answer “six hundred three-ty fifteen” now appears. This is still a lovely, mathematically correct answer. But society at large might not agree. Let’s do another explosion: ten dots in the rightmost box.
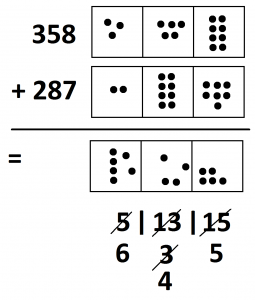
Now we see the answer “six hundred four-ty five,” which is one that society understands. (Although, in English, “four-ty” is usually spelled forty.)
Here are some practice problems you might or might not want to try. My solutions to them appear in the final section of this experience.
1. Write down the answers to the following addition problems working left to right and not worrying about what society thinks! Then, do some explosions to translate each answer into something society understands.
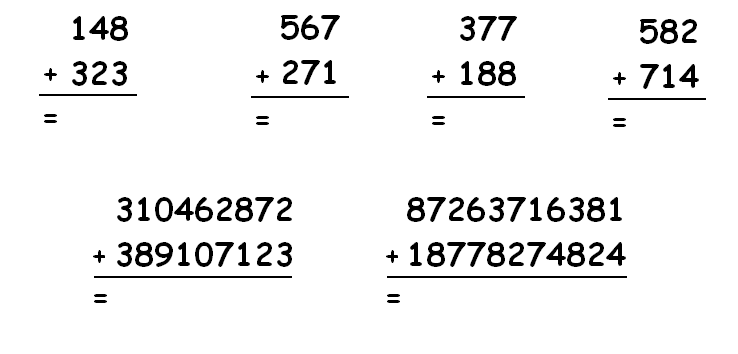
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()


