See how Goldfish & Robin, “When Young Minds Collide,” explain this lesson: Kids Explain Math for Kids.  

 

My disbelief in subtraction comes from another story that isn’t true. Briefly, it goes as follows.

As a young child I used to regularly play in a sandbox. And there I discovered the positive counting numbers as piles of sand: one pile, two piles, and so on. And I also discovered the addition of positive numbers simply by lining up piles. For example, I saw that two plus three equals five simply by lining up piles like this.

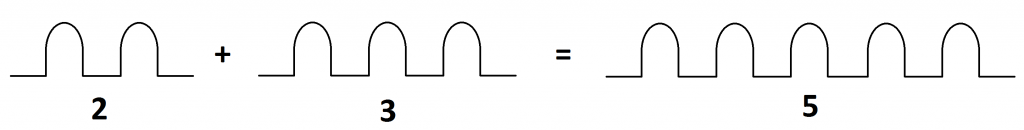
I had hours of fun counting and lining up piles to explore addition.

But then one day I had an astounding flash on insight! Instead of making piles of sand, I realized I could also make holes. And I saw right away that a hole is the opposite of a pile: place a pile and a hole together and they cancel each other out. Whoa!

Later in school I was taught to call a hole “\(-1\)”, and two holes “\(-2\),” and so on and was told to do this thing called “subtraction.” But I never really believed in subtraction. My colleagues would read \(5-2\), say, as ”five take away two,” but I was thinking of five piles and the addition of two holes. A picture shows that the answer is three piles.

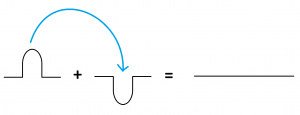
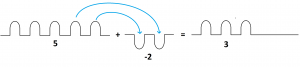
Yes. This gives the same answer as my peers, of course: the two holes “took away” two of the piles. But I had an advantage. For example, my colleagues would say that \(7-10\) has no answer. I saw that it did.

\(7-10 = \)  seven piles and ten holes \(=\) three holes \( = -3\).

Easy!

Subtraction is just the addition of the opposite.

(By the way, I will happily write \(7-10\) as “\(7 + \; -10\).” This makes the thinking more obvious.)

 

 

Let’s go back now to our dots-and-boxes machines, the \(1 \leftarrow 10\) machine in particular.

 

There we work with dots, which I’ve been drawing as solid dots.

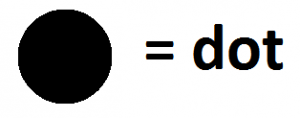
We now need the notion of the opposite of dot, like a hole is the opposite of a pile. I’ll draw the opposite of a dot as a hollow circle and call it an antidot.

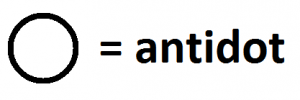
Like matter and antimatter, and like \(1\) and \(-1\)  in piles and holes, which each annihilate one another when brought together, a dot and an antidot should also annihilate too – POOF! – when brought together to leave nothing behind.

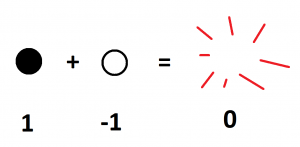
And we can conduct basic arithmetic with dots and antidots, just like we did with piles and holes.

 

Aside: By the way, some students prefer to call the opposite of a dot a tod. Can you guess what made them think of that name?

Resources