See how Goldfish & Robin and Friends, “Math on the Menu,” explain subtraction: Kids Explain Math for Kids. 

Consider this subtraction problem.

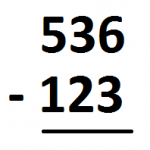
To me, this is \(536\) plus the opposite of \(123\).

The first number, \(536\), looks like this in a \(1 \leftarrow 10\) machine: five dots, three dots, six dots.

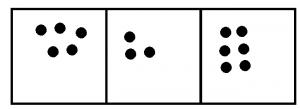
 To this we are adding the opposite of \(123\). That is, we’re adding one anti-hundred, two anti-tens, and three anti-ones.

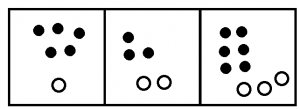
 And now there are a lot of annihilations.: POOF!;  POOF POOF!;  POOF POOF POOF!

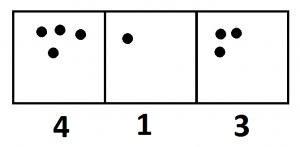
We see the answer \(413\) appear.

And notice, we get this answer as though we just work left to right and say

\(5\) take away \(1\) is \(4\),

\(3\) take away \(2\) is \(1\),

and

\(6\) take away \(3\) is \(3\).

Yes! Left to right again!

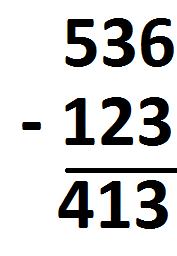
All right. That example was too nice. How about \(512 – 347\)?

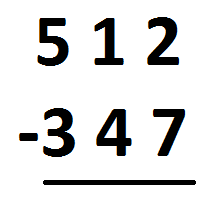
Going from left to right, we get: \(5\) take away  \(3\) is \(2\), \(1\) take away \(4\) is \(-3\), and \(2\) take away \(7\) is \(-5\). The answer is two-hundred negative-three-ty negative-five.

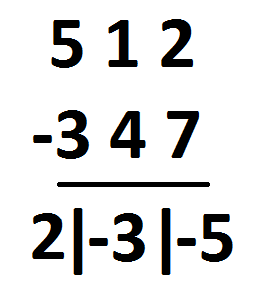
And this answer is absolutely mathematically correct! I picture shows it is.

Here’s five hundreds, one ten and two ones together with three anti-hundreds, four anti-tens, and seven anti-ones.

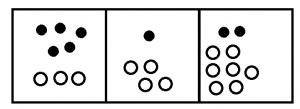
And after lots of annihilations we get are left with two actual hundreds, three anti-tens, and five anti-ones.

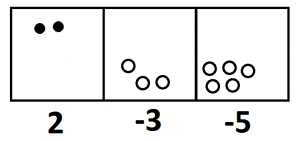
The answer really is two-hundred negative-three-ty negative-five!

But, of course, saying the answer to our subtraction problem this way seems mighty weird to society. Can we fix up this mathematically correct answer for society’s sake?

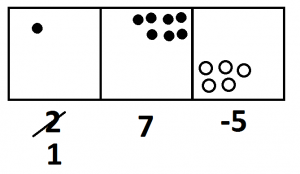
It takes a flash of insight to realize that we can “unexplode” dots: any dot in a box to the left must have come from ten dots in the box just to its right.

Okay. Let’s unexplode one of the two dots we have in the leftmost box. Doing so gives this picture.

After annihilations, we see we now have the answer one-hundred seventy negative-five. Beautiful!

Let’s unexplode again.

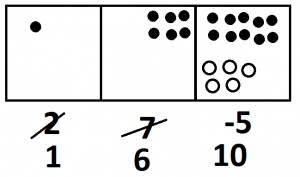
And with some more annihilations we see an answer society can understand: one-hundred sixty five.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources