How does this dots-and-boxes approach compare with the standard algorithm?

Consider again \(512-347\).

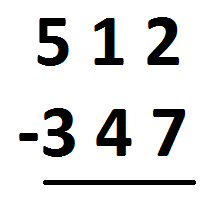
The standard algorithm has you start at the right to first look at “\(2\) take away \(7\),” which you can’t do.

(Well you can do it, it is \(-5\), but you are not to write that for this algorithm.)

So what do you do?

You “borrow one.” That is, you take a dot from the tens column and unexplode it to make ten ones. That leaves zero dots in the tens column.  We should write ten ones to go with the two in the ones column.

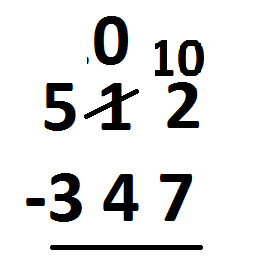
But we are a bit clever here and just write \(12\) rather than \(10+2\). (That is, we put a \(1\) in front of the \(2\) to make it look like twelve.)

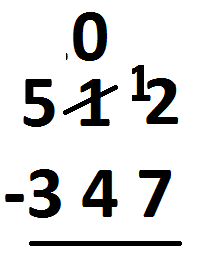
Then we say “twelve take seven is five” and write that answer.

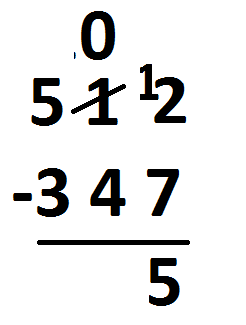
The rightmost column is complete. Shift now to the middle column.

We see “zero take away four,” which can’t be done. So perform another unexplosion, that is, another “borrow,” to see \(10-4\) in that column. We write the answer \(6\).

We then move to the last remaining column where we have \(4-3\), which is \(1\).

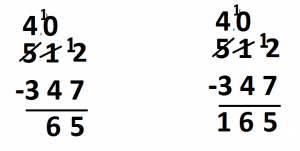
Phew!

Here is a question for you to try, if you like. My answer to it appear in the final section of this chapter.

1. Compute each of the following two ways: the dots-and-boxes way (and fixing the answer for society to read) and then with the traditional algorithm. The answers should be the same.

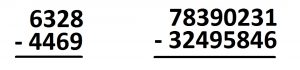
Thinking question along the way: As you fix up your answers for society, does it seem easier to unexplode from left to right, or from right to left?

Additional question:  Do you think you could become just as speedy the dots-and-boxes way as you currently are with the traditional approach?

Again. All correct approaches to mathematics are correct, and it is just a matter of style as to which approach you like best for subtraction. The traditional algorithm has you work from right to left and do all the unexplosions as you go along. The dots-and-boxes approach has you “just do it!” and conduct all the unexplosions at the end.  Both methods are fine and correct.

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources