Division is linked with multiplication. In fact, many people think of division as the reverse of multiplication. So let’s revisit multiplication for a moment to then see if we can follow it backwards to get to division. We’ll start with a straightforward multiplication problem, say, \(1302 \times 3\) (with answer \(3906\)).

Here’s what \(1302\) looks like in a \(1 \leftarrow 10\) machine.  (I’ve colored the dots for fun.)

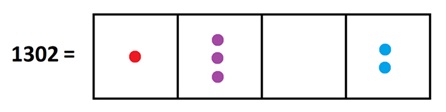
To triple this quantity, we just need to replace each dot in the picture with three dots. We see the answer \(3906\).

Now suppose I gave you the second picture first and said “Please use it to divide \(3906\) by three.” Could you use the picture to see triples of dots that must have come from single dots? Yes! Look at the picture this way.

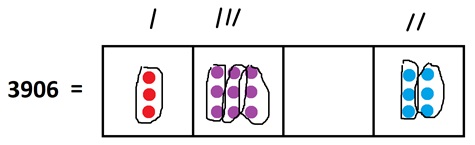
We see the picture as the result of tripling one dot at the thousands level, tripling three dots at the hundreds level, and tripling two dots at the ones level. That is, we see \(3906\) as the number \(1302\) tripled.

We have just deduced, from the picture, that \(3906 \div 3=1302\)!

 

Thinking Question: What would you deduce if you look at the same picture this way?

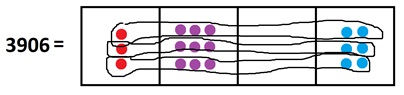
(Warning: This picture is neat to see. But we were lucky there were no explosions to obscure the pattern. In more complicated pictures, it might be trickier to look at our pictures in this horizontal way.)

 

Here are some practice problems you might or might not want to try. (My answers to them are at the end of this experience.)

 

1. Draw a dots and boxes picture of the number \(426\) and use it to explain why \(426 \div 2\)  equals \(213\) .

2. Try doing \(402 \div 3\) with just a dots-and-boxes picture. Do you see that unexplosions unlock this problem to reveal the answer \(134\)?

3. You just showed that \(402 \div 3 = 134\) . What do you think is the answer, then, to \(404 \div 3\)? What would you see in a picture of this division problem?

 

So, to divide a number by three, all we need to do is to look for groups of three in the picture of the number. Each group of three corresponds to a dot that must have been tripled.  We can just read off the answer to the division problem then by looking at the groups we find!

Of course, we can do the same for any single digit division problem.

 

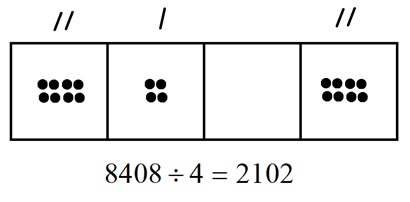
4. Compute \(61230 \div 5\) by the dots-and-boxes approach. (Does it get tiresome drawing dots? Do you have to actually draw them?)

 

Multi-Digit Division

Division by single-digit numbers is all well and good. What about division by multi-digit numbers? People usually call that long division.

 

Let’s consider the problem \(276 \div 12\).

 

Here is a picture of \(276\) in a \(1 \leftarrow 10\) machine.

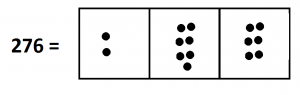
And we are looking for groups of twelve in this picture of  \(276\). Could this be the result of a different picture whose single dots were each replaced by a group of twelve?

Here’s what twelve looks like.

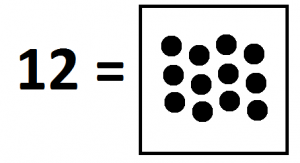
Actually, this is not quite right as there would be an explosion in our \(1 \leftarrow 10\) machine. Twelve will look like one dot next to two dots. (But we need to always keep in mind that this really is a picture with all twelve dots residing in the rightmost box.)

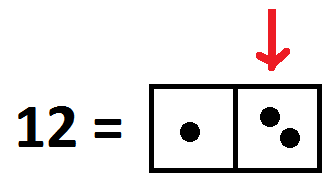
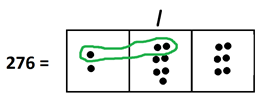
Okay. So we’re looking for groups of \(12\) in our picture of \(276\). Do we see any one-dot-next-to-two-dots in the diagram?

 

Yes. Here’s one.

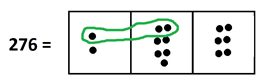
Within each loop of \(12\) we find the \(12\) dots actually reside in the right part of the loop. So we have found one group of \(12\) at the tens level.

And there are more groups of twelve.

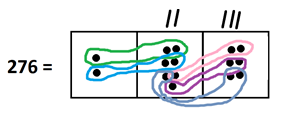
This shows that our picture of \(276\) is actually a picture of \(23\) each of whose dots was replaced by \(12\). We see \(276 = 23 \times 12\) and so \(276 \div 12 = 23\).

 

Alternatively, we can say in our picture of \(276\) we’ve identified two groups of \(12\) at the tens level and three \(12\)s at the ones level, and so there are \(23\) groups of \(12\) in \(276\).

No matter how you wish to interpret matters, the picture reveals all!

 

Here are some practice questions you might, or might not, want to try. My answers to them appear in the final section of this experience.

 

5. Compute \( 2783 \div 23\) by the dots-and-boxes approach by hand.

6. Compute \(3900 \div 12\).

 

 

Let’s do another example. Let’s compute \(31824 \div 102\).

 

Here’s the picture.

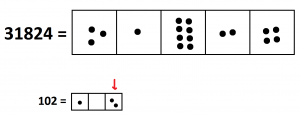
Now we are looking for groups of one dot–no dots–two dots in our picture of \(31824\). (And, remember, all \(102\) dots are physically sitting in the rightmost position of each set we identify.)

 

We can spot a number of these groups. (I now find drawing loops messy so I am drawing Xs and circles and boxes instead. Is that okay? Do you also see how I circled a double group in one hit at the very end?)

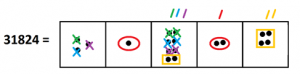
The answer \(312\) to \(31824 \div 102\) is now apparent. (The colors show that \(31824\) is a picture of \(312\) with each dot multiplied by \(102\). Or, if you prefer, we’ve found \(312\) groups of \(102\) in our picture of \(31824\).)

 

 

Here are some more questions to try, if you wish.

 

7. Compute \(46632 \div 201\).

8. Show that \( 31533 \div 101\) equals \(312\) with a remainder of \(21\). 

 

 

Resources