Exploding Dots
6.8 Wild Explorations
Here are some “big question” investigations you might want to explore, or just think about. Have fun!
| EXPLORATION 1: CAN WE EXPLAIN AN ARITHMETIC TRICK?
Here’s an unusual way to divide by nine.
To compute \(21203 \div 9\), say, read “\(21203\)” from left to right computing the partial sums of the digits along the way
and then read off the answer \(21203\div 9 = 2355 \; R8\). In the same way, \(1033 \div 9 = 114 \; R7\) and \(2222 \div 9 = 246 \; R8\).
Can you explain why this trick works?
Here’s the approach I might take: For the first example, draw a picture of \(21203\) in a \(1 \leftarrow 10\) machine, but think of nine as \(10-1\). That is, look for copies of
in the picture.
|
| EXPLORATION 2: CAN WE EXPLORE NUMBER THEORY?
Use an \(1 \leftarrow x\) machine to compute each of the following
a) \(\dfrac{x^{2}-1}{x-1}\) b) \(\dfrac{x^{3}-1}{x-1}\) c) \(\dfrac{x^{6}-1}{x-1}\) d) \(\dfrac{x^{10}-1}{x-1}\)
Can you now see that \(\dfrac{x^{number}-1}{x-1}\) will always have a nice answer without a remainder?
Another way of saying this is that \(x^{number}-1 = \left(x-1\right) \times \left(something\right)\).
For example, you might have seen from part c) that \(x^{6}-1 = \left(x-1\right)\left(x^{5}+x^{4}+x^{3}+x^2+x+1\right)\). This means we can say, for example, that \(17^{6}-1\) is sure to be a multiple of \(16\)! How? Just choose \(x=17\) in this formula to get
\(17^{6}-1 = \left(17-1\right) \times \left(something\right)=16\times \left(something\right) \).
a) Explain why \(999^{100}-1\) must be a multiple of \(998\).
b) Can you explain why \(2^{100}-1\) must be a multiple of 3, and a multiple of 15, and a multiple of 31 and a multiple of 1023? (Hint: \(2^{100}=\left(2^2\right)^{50}=4^{50}\), and so on.)
c) Is \(x^{number}-1\) always a multiple of \(x+1\)? Sometimes, at least?
d) The number \(2^{100}+1\) is not prime. It is a multiple of \(17\). Can you see how to prove this? |
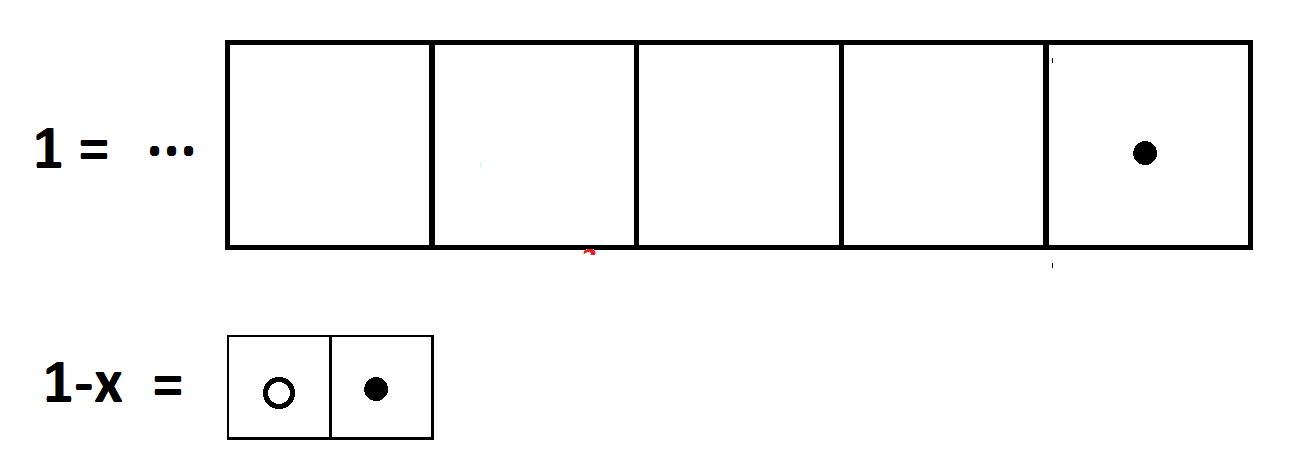
| EXPLORATION 3: AN INFINITE ANSWER?
Here is a picture of the very simple polynomial \(1\) and the polynomial \(1-x\).
Can you compute \(\dfrac{1}{1-x}\)? Can you interpret the answer? (We’ll explore this example in the next chapter.) |
| EXPLORATION 4: LONG MULTIPLICATION IN ANY BASE!
Math enthusiast Baron Hansz has described an terrific way to perform long multiplication in any base you like — even fractional ones — with absolute ease! He brilliantly combines the area model with Exploding Dots thinking. This video bounces of his video, giving my take on explaining Baron’s lovely approach. Her’s my take on explaining Baron’s lovely approach.
And here’s Baron’s video with the fellow himself explaining his method.
What do you think of this approach? |
Resources
Books
Take your understanding to the next level with easy to understand books by James Tanton.
BROWSE BOOKS![]()
Guides & Solutions
Dive deeper into key topics through detailed, easy to follow guides and solution sets.
BROWSE GUIDES![]()
Donations
Consider supporting G'Day Math! with a donation, of any amount.
Your support is so much appreciated and enables the continued creation of great course content. Thanks!
Ready to Help?
Donations can be made via PayPal and major credit cards. A PayPal account is not required. Many thanks!
DONATE![]()