Let’s go back to working with a \(1 \leftarrow 10\) machine and see what boxes to the right could mean in that machine. (Then it should become clear what they mean in other machines as well.)

 

To keep the left and right boxes visibly distinct, we’ll separate them with a point. (Society calls this point, for a \(1 \leftarrow 10\) machine at least, a decimal point.)

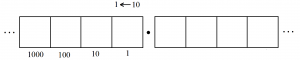
So, what does it mean to have dots in the right boxes? What are the values of dots in those boxes?

Since this is a \(1 \leftarrow 10\) machine, we do know that ten dots in any one box explode to make one dot one place to the left. So ten dots in the box just to the right of the decimal point are equivalent to one dot in the \(1\)s box.  Each dot in that box must be worth one-tenth.

We have our first place value to the right of the decimal point.

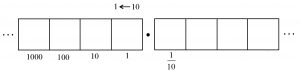
In the same way, ten dots in the next box over are worth one-tenth. And so each dot in that next box must be worth one-hundredth.

We now have two place values to the right of the decimal point.

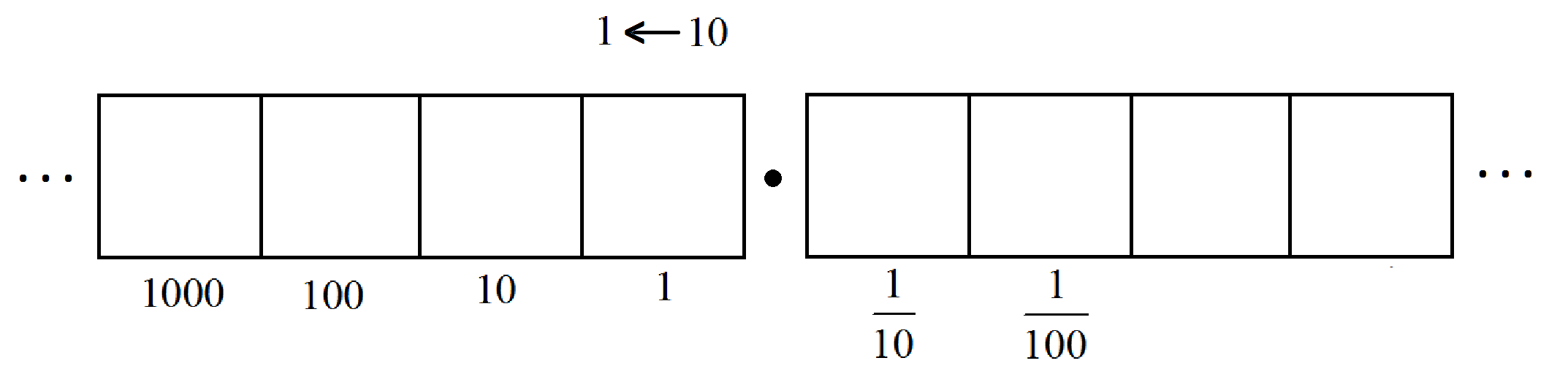
And ten one-thousandths make a hundredth, and ten ten-thousandths make a thousandth, and so on.

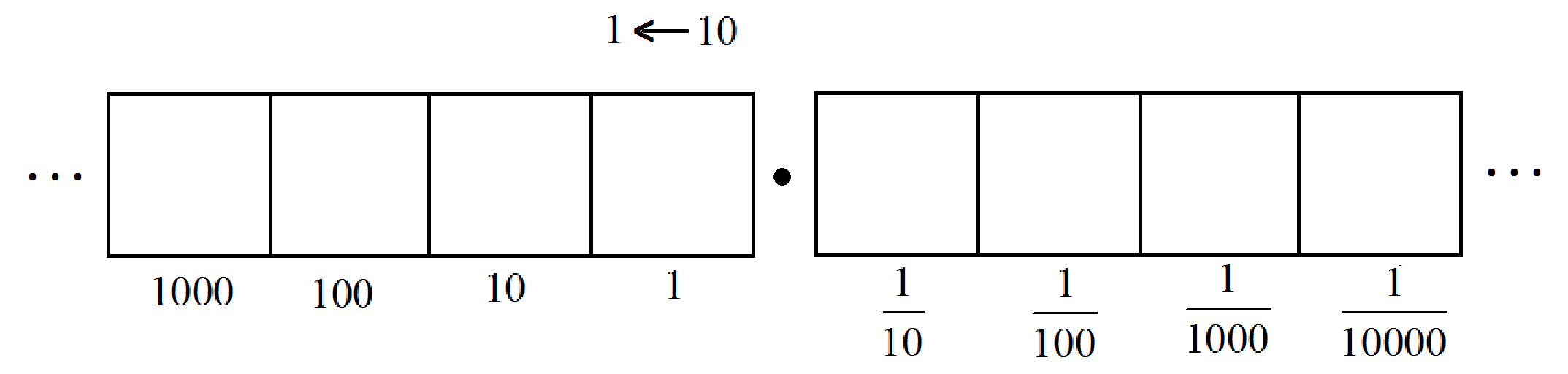
We see that the boxes to the left of the decimal point represent place values as given by the powers of ten, and the boxes to the right of the decimal point represent place values given by the reciprocals of the powers of ten.

 

We have just discovered decimals!

 

Question: What does the prefix deci mean in English? Would we talk about “decimals” in a \(1 \leftarrow 2\) machine, for instance? (And why isn’t December the tenth month of the year? What happened in the history of the western calendar?)

 

When people write \(0.3\), for example, in base ten, they mean the value of placing three dots in the first box after the decimal point.

 We see that \(0.3\) equals three tenths: \(0.3 = \dfrac{3}{10}\).

 

Seven dots in the third box after the decimal point is seven thousandths: \(0.007=\dfrac{7}{1000}\).

 

Comment: Some people might leave off the beginning zero and just write \(.007=\dfrac{7}{1000}\). It’s just a matter of personal taste.

 

Here’s a question. I’ve included my answer to it, and the answers to all the other questions I sprinkle throughout this chapter, in the final section.

 

1. Some people read \(0.6\) out loud as “point six” and others read it out loud as “six tenths.” Which is more helpful for understanding what the number really is?

 

There is a possible source of confusion with a decimal such as \(0.31\). This is technically three tenths and one hundredth: \(0.31=\dfrac{3}{10}+\dfrac{1}{100}\).

But some people read  out loud as “thirty-one hundredths,” which looks like this.

Are these the same thing?

 

Well, yes! With three explosions we see that thirty-one hundredths becomes three tenths and one hundredth.

 

Comment: You can also show that \(\dfrac{3}{10}+\dfrac{1}{100}\) and \(\dfrac{31}{100}\) are the same with the arithmetic of adding fractions. We have \(\dfrac{3}{10}+\dfrac{1}{100}=\dfrac{30}{100}+\dfrac{1}{100}=\dfrac{31}{100}\).  (Do you see that this is really the result of performing three unexplosions in a picture of \(\dfrac{3}{10}+\dfrac{1}{100}\)

 

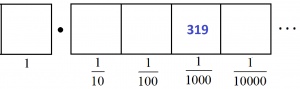
2. A teacher asked his students to each draw a \(1 \leftarrow 10\) machine picture of the fraction \(\dfrac{319}{1000}\).

JinJin drew:

Subra drew:

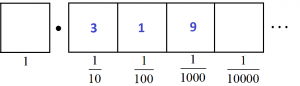
The teacher marked both students as correct. Are each of these solutions indeed valid? Explain your thinking. (By the way, the teacher doesn’t mind if students just write numbers instead of drawing dots.)

 

3. Multiple choice!

     a) The decimal \(0.23\) equals: (A) \(\dfrac{23}{10}\)  (B) \(\dfrac{23}{100}\)    (C) \(\dfrac{23}{1000}\)   (D) \(\dfrac{23}{10000}\)?

     b) The decimal \(0.0409\) equals: (A) \(\dfrac{409}{100}\)   (B) \(\dfrac{409}{1000}\)   (C) \(\dfrac{409}{10000}\)   (D) \(\dfrac{409}{100000}\)?

 

 

SIMPLE FRACTIONS AS DECIMALS

Some decimals give fractions that simplify further. For example,

\(0.5=\dfrac{5}{10}=\dfrac{1}{2}\)

and

\(0.04=\dfrac{4}{100}=\dfrac{1}{25}\).

 

Conversely, if a fraction can be rewritten to have a denominator that is a power of ten, then we can easily write it as a decimal. For example,

\(\dfrac{3}{5}=\dfrac{6}{10}\)  and so \(\dfrac{3}{5}=0.6\)

and

\(\dfrac{13}{20}=\dfrac{13 \times 5}{20 \times 5}=\dfrac{65}{100}=0.65\).

 

Here are some more problems. Do whichever ones seem interesting to you.

 

4. What fractions (in simplest terms) do the following decimals represent?

\(0.05\)     \(0.2\)     \(0.8\)     \(0.004\)

 

5. Write each of the following fractions as a decimal.

\(\dfrac{2}{5}\)     \(\dfrac{1}{25}\)     \(\dfrac{1}{20}\)     \(\dfrac{1}{200}\)     \(\dfrac{2}{2500}\)

 

6. Multiple choice!

a) The decimal \(0.050\) equals (A) \(\dfrac{50}{100}\)   (B) \(\dfrac{1}{20}\)    (C) \(\dfrac{1}{200}\)     (D) None of these

b) The decimal \(0.000208\) equals (A) \(\dfrac{52}{250}\)     (B) \(\dfrac{52}{2500}\)     (C) \(\dfrac{52}{25000}\)     (D) \(\dfrac{52}{250000}\)

 

7. Write each of the following fractions as decimals.

\(\dfrac{7}{20}\)     \(\dfrac{16}{25}\)     \(\dfrac{301}{500}\)     \(\dfrac{17}{50}\)     \(\dfrac{3}{4}\)

 

8. CHALLENGE

a) What fraction does the decimal \(2.3\) represent?

b) What fraction does \(17.04\)represent?

c) What fraction does \(1003.1003\) represent?

 

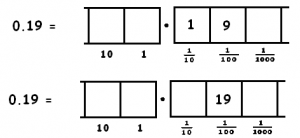
9. Let’s explore the question: Do \(0.19\)and \(0.190\) represent the same number or different numbers?

Here are two dots and boxes pictures for the decimal 0.19:

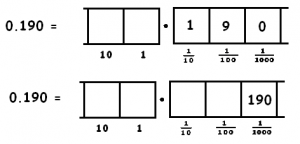
Here are two dots and boxes picture for the decimal 0.190

a) Explain how one “unexplosion” establishes that the first picture of \(0.19\) is equivalent to the second picture of \(0.19\).

b) Explain how several unexplosions establishes that the first picture of \(0.190\) is equivalent to the second picture of \(0.190\).

c) Explain how explosions and unexplosions in fact establish that all four pictures are equivalent to each other.

d) In conclusion then: Does \(0.190\) represent the same number as \(0.19\)?

 

To a mathematician, the expressions \(0.19\) and \(0.190\) represent exactly the same numeric quantity. But you may have noticed in science class that scientists will often write down what seems likes unnecessary zeros when recording measurements. This is because scientists want to impart more information to the reader than just a numeric value.

 

For example, suppose a botanist measures the length of a stalk. By writing the measurement as \(0.190\) meters in her paper, the scientist is saying to the reader that she measured the length of the stalk to the nearest one thousandth of a meter and that she got \(1\) tenth, \(9\) hundredths, and \(0\) thousandths of a meter. Thus we are being told that the true length of the stalk is somewhere in the range of \(0.1895\) and \(0.1905\) meters.

 

If she wrote in her paper, instead, just \(0.19\) meters, then we would have to assume she measured the length of the stalk only to the nearest hundredth of a meter and so its true length lies somewhere between \(0.185\) and \(0.195\) meters.

 

 

MIXED NUMBERS AS DECIMALS

 How does \(12\dfrac{3}{4}\), for example, appear as a decimal?

 

Well, \(12\dfrac{3}{4}=12+\dfrac{3}{4}\) and we can certainly write the fractional part as a decimal. (The non-fractional part is already in the \(1 \leftarrow 10\) machine format!) We have

\(12\dfrac{3}{4}=12+\dfrac{75}{100}\)

and so we see

\(12\dfrac{3}{4}=12.75\).

 

10. Write each of the following numbers in decimal notation.

\(5\dfrac{3}{10}\)     \(7\dfrac{1}{5}\)     \(13\dfrac{1}{2}\)     \(106\dfrac{3}{20}\)     \(\dfrac{78}{25}\)     \(\dfrac{9}{4}\)     \(\dfrac{131}{40}\)

 

 

Resources