Even though the addition and subtraction of decimals is straightforward in a \(1 \leftarrow 10\) machine, performing multiplication and division on them can be awkward. The trouble is that the \(1 \leftarrow 10\) machine is based on whole dots, not parts of dots, and so it is tricky to make easy sense of pictures.  But there are ways to play with dots-and-boxes nonetheless.

 

MULTIPLICATION

We can certainly do some basic multiplication. For example, a picture of dots and boxes shows that \(2.615 \times 7\) equals \(14.42|7|35\).

With explosions, this becomes \(18.305\). (Check this!)

 

We can also explain a rule that students are taught to memorize:

 

If you multiply a decimal by \(10\), just shift the decimal point one place to the right.

 

For example, \(3.42 \times 10\) gives the answer \(30|10.40|20\). With explosions, this becomes \(314.20\) and the answer looks as though we just shifted the decimal point. (Most people leave off the final zero.)

By the way, if you multiply a number a little larger than \(31\) by ten, you should get an answer a little larger than \(310\). Memorizing the direction of travel of a decimal point is unnecessary.

 

13. Explain why multiplying a decimal by \(100\) has the same effect as shifting the decimal point two places? (Do you need to memorize the direction of the shift?)

 

We can also multiply decimals by decimals, but now the work is getting less fun. We need to follow the same approach as we did when we explored long multiplication in chapter 3.

 

Let’s do an example. Consider \(2.15 \times 0.3\).

 

Here’s what \(2.15\) looks like.

Here’s what \(0.3\) looks like: it’s three dots to the right of where one dot should be.

 

So to compute \(2.15 \times 0.3\) we need to replace each dot that appears in the picture of \(2.15\) with three dots to the right of where that dot should be. Doing so gives this picture.

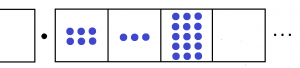
We see the answer \(0.6|3|15\), or  after an explosion \(0.645\).

 

So multiplication with decimals is doable, but awkward. It is actually easier, in practice, to go back to basic arithmetic and work with decimals as fractions. For example,

 

\(0.2 \times 0.4 = \dfrac{2}{10} \times \dfrac{4}{10} = \dfrac{8}{100} =  0.08\)

and

\(0.05 \times 0.006 = \dfrac{5}{100} \times \dfrac{6}{1000} = \dfrac{30}{100000} = \dfrac{3}{10000}=0.0003\)

and

\(2.15 \times 0.3 = \left(2+\dfrac{15}{100}\right) \times \dfrac{3}{10}=\dfrac{6}{10}+\dfrac{45}{1000}=0.6+0.045-0.645\).

 

We also see the effect of multiplying a decimal by ten this way. For example

 

\(10 \times 3.142 = 10 \times \left(3+\dfrac{1}{10}+\dfrac{4}{100}+\dfrac{2}{1000}\right)=30+1+\dfrac{4}{10}+\dfrac{2}{100}=31.42\).

 

 

14. Compute \(0.04 \times 0.5\) and compute \(1000 \times 0.0385\).

 

 

DIVISION

Consider \(0.08 \div 0.005\).

 

To do this problem I could try drawing a picture of \(0.08\) in a \(1 \leftarrow 10\) machine and attempt to make sense of finding groups of \(0.005\) in that picture, that is groups of five dots three places to the right of where they should be. Although possible to do, it seems hard to keep straight in my head and it makes my brain hurt!

 

Here’s a piece of advice from a mathematician: Avoid hard work!  Mathematicians will, in fact, work very hard to avoid hard work!

 

Since converting decimals to fractions makes the multiplication of fractions easier, let’s do the same thing for division.

 

Here are some examples.

 

Example: Examine \(0.08 \div 0.005\).

 

A fraction is a number that is an answer to a division problem. And, conversely, we can think of a division problem as a fraction. For example, the quantity \(0.08 \div 0.005\) is really this “fraction”

 

\(\dfrac{0.08}{0.005}\).

 

(It is okay to have non-whole numbers as numerators and denominators of fractions.)

 

To make this fraction look friendlier, let’s multiply the top and bottom by factors of ten.

 

\(\dfrac{0.08\times 10 \times 10 \times 10}{0.005 \times 10 \times 10 \times 10}=\dfrac{80}{5}\)

 

 

The division problem \(\dfrac{80}{5}\) is much friendlier. It has the answer \(16\). (Use a \(1 \leftarrow 10\) machine now to compute it if you like!)

 

Example: Examine \(\dfrac{8.5}{100}\).

 

Dividing by \(100\) is the same as multiplying by \(\dfrac{1}{100}\). So, \(\dfrac{8.5}{100}\), for example, can be thought of as

 

\(\dfrac{1}{100} \times 8.5= \dfrac{1}{100}\left(8+\dfrac{5}{10}\right)= \dfrac{8}{100}+\dfrac{5}{1000}=0.085\).

 

Of course, we can also think of this as \(\dfrac{8.5 \times 10}{100 \times 10}=\dfrac{85}{1000}\), which seems more direct. (All correct paths in mathematics are good and correct!)

 

Example: Examine \(1.51 \div 0.07\).

 

If I was asked to compute \(1.51 \div 0.07\), I would personally do this problem instead:

 

\(\dfrac{1.51 \times 10 \times 10}{0.07 \times 10 \times 10}=\dfrac{151}{7}\).

 

I see the answer \(21\dfrac{4}{7}\).  If that same person asked me to give the answer as a decimal, then I would have to convert the fraction \(\dfrac{4}{7}\) into a decimal. And that is possible. The next section explains how!

 

15. Explain why the answer to \(0.9 \div 10\) must be \(0.09\).

      Explain why the answer to \(2.34 \div 1000\) must be \(0.00234\).

      Explain why the answer to \(40.04 \div 0.01\) must be \(4004\).

 

16. Compute \(\dfrac{0.75}{25}\).

 

17. Let’s put it all together. Here are some unpleasant computations. Do you want to try evaluating them?

a) \(0.3 \times \left(5.37-2.07\right)\)

b) \(\dfrac{0.1+\left(1.01-0.1\right)}{0.11+0.09}\)

c) \(\dfrac{\left(0.002+0.2 \times 2.02\right)\left(2.2-0.22\right)}{2.22-0.22}\)

 

 

 

Resources