[My thanks to James Key for suggesting this opening.]

Here are three problems:

1. Ten people in an office. Their boss one day decides to randomly select three people and give them each a promotion. How many different possible groups of three are there?

2. Ten people in an office. Their boss one day decides to randomly select three people and give them each a promotion. The first selected will receive a top promotion, the second selected an average promotion, and the third a minimal promotion. In how many different ways could these promotions be assigned?

3. Ten people in an office. Their boss, one day, decides to randomly select six people and give them each a promotion. Two will receive top promotions, one an average promotion, and three a minimal promotion. In how many different ways could these promotions be assigned?

The method for answering each question is the same.

Imagine all ten office folk standing in a line.

In the first problem, the boss calls three people “promoted” (P) and seven “not promoted” (N). We need to count all the ways she could assign these labels for ten people in a line.  The list of possibilities, each the labels assigned in that line, looks like:

So to answer the question we need to count the number of “words” composed of three Ps and seven Ns.

In the second problem, the boss calls one person “top promoted” (T), one person “average promoted” (A), one person “minimally promoted” (M), and seven “not promoted” (N). We need to count all the ways she could assign these labels for ten people in a line.  The list of possibilities looks like:

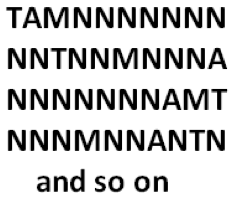
So to answer the question we need to count the number of “words” composed of one T, one A, one M, and seven Ns.

In the third problem, the boss calls two people “top promoted” (T), one person “average promoted” (A), three people “minimally promoted” (M), and four “not promoted” (N). We need to count all the ways she could assign these labels for ten people in a line.  The list of possibilities looks like:

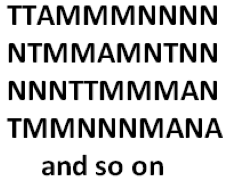
So to answer the question we need to count the number of “words” composed of two Ts, one A, three Ms, and four Ns.

All three problems are essentially the same:  How many ways can we arrange letters of a word?

Assigning labels in a counting problem makes all counting challenges identical!

So our job in this course is simply to learn how to count rearrangements of letters in words!

Please join the conversation on Facebook and Twitter and kindly share this page using the buttons below.

Facebook

Twitter

Resources