Loosely speaking, the area of a geometric figure is the amount of space inside it. Such a definition appeals to our intuitive understanding. What is that intuitive understanding exactly?

 

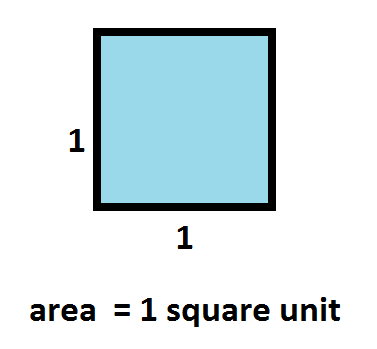
A study of area usually begins by declaring the area of a square one unit wide to be one square unit. We call this a basic unit of area.

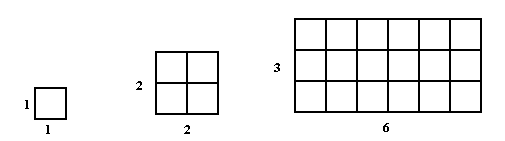
As four of these basic units fit snugly into a square with side-length two, without overlap, we say then that a \(2 \times 2\) square has area four. Similarly, a \(3 \times 3\) square has area nine, a \(4 \times 4\) square area \(16\), and so on.

A \(3 \times 6\) rectangle holds \(18\) basic unit squares and so has area \(18\). In general, a rectangle that is \(a\) units long and \(b\) units wide, with both \(a\) and \(b\) whole numbers, has area \(a \times b\). Young students explore this idea in the K-5 curriculum.

As four \(\frac{1}{2}\times\frac{1}{2}\) squares fit snugly in a unit square, we say that the area of such a small square is \(\frac{1}{4}\) square units.

And further exploration in cutting fractions of unit squares seems to indicate that the area of an \(a\)-by-\(b\) rectangle is \(a \times b\) square units, even if \(a\) and \(b\) possess fractional parts.

This has the feel of a general fundamental fact. It feels so natural and right, that we could deem this to be the very starting point of a general theory of area.

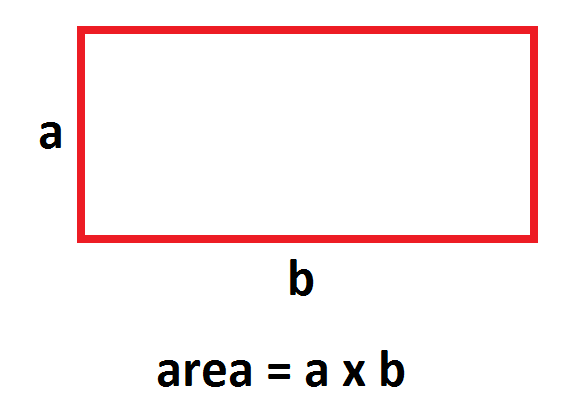
DEFINITION: The area of a rectangle shall be defined as the product of its length and its width.

A Comment for us Adults: This definition is taken as an observation in the K-5 curriculum (all quantities discussed there are either whole numbers or fractions). But for those who know of the existence of irrational numbers, this definition takes matters to a next level: Although it is impossible to fit a whole number or even a fractional number of unit squares into a rectangle that is \(5 \frac{3}{4}\) units long and \(\sqrt{7}\) units wide, for example, we are declaring, nonetheless, that the area of such a rectangle is the product of these two numbers. This is bold!  Fortunately, this claim matches our intuitive idea belief that, with the aid of scissors, about \(5\frac{3}{4} \times \sqrt{7} \approx 15.213\) unit squares will fit in this rectangle. (We as humans, however, will never see the truly correct proportion of unit squares that fit in this shape. The claim then is indeed bold.)

 

For a proper theory of area we must also make some fundamental assumptions about how area works. Watch this paradoxical video to see how I motive the following two dry ideas via quirky intrigue.

It seems reasonable to say that two rectangles that overlap only along a shared edge produce a figure with area the sum of the areas of the rectangles.

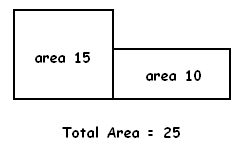
Many take this as a fundamental postulate of geometry:

Area Addition Postulate: If a figure can be regarded as the union of two smaller figures that overlap along only along line segments, then the total area of the figure is the sum of the areas of the smaller figures.

This is, of course, assuming we have a meaningful concept of what area means for those two smaller figures.

We also like to believe:

Area Congruence Postulate: Two congruent figures have the same area.

That is, the area of a figure does not change under translation, rotation, or reflection.

These two beliefs, taken as observations in the K-5 curriculum and taken as axioms in high-school geometry, along with the defining definition of the area of a rectangle are enough to develop a meaningful theory of area for all of middle-school and high-school mathematics: we can now derive formulas for the areas of parallelograms, triangles, regular polygons, and so on. (See the video and my GEOMETRY texts for details on developing all this work.)

 

Let’s now solve some introductory mathematics problems with an area-thinking approach.

 

Example: A juice blend consists of 60% apple juice, 30% pear juice, and 10% mixed berry juice. A juice cocktail contains 50% apple juice, 10% cherry juice, and 40% water. If two gallons of juice blend are mixed with three gallons of juice cocktail, give the percentage of each type of juice and water in the five-gallon mixture.

Answer:

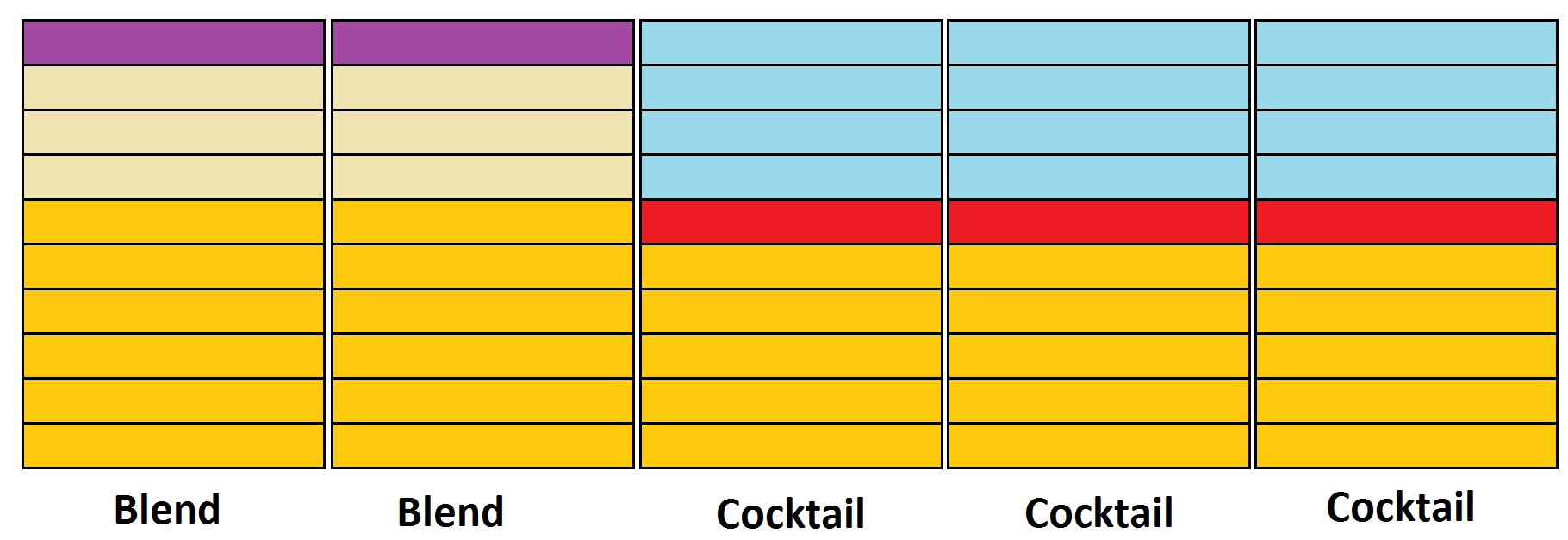
We see that the five gallons consists of \(6+6+5+5+5=27\) parts out of fifty, that is \(54\%\), apple juice, \(\frac{6}{50}=12\%\) pear juice, \(\frac{2}{50}=4\%\) berry juice, \(\frac{3}{50}=6\%\) cherry juice, and \(\frac{12}{50}=24\%\) water.

    

Exercise: In the previous question, how many gallons of juice cocktail mixed with two gallons of juice blend will give a mixture that is 45% apple juice? 30% apple juice?

 

Example:  In a certain college, \(60\%\) of the students are women and  \(40\%\) are men. Of the women, \(50\%\) are working towards a degree in math; of the men, \(25\%\). What percentage of college students are math majors?

Answer:

We see that \(40\%\) of the college students are math majors.

 

Exercise: Suppose we switch the numbers in the previous question: In a certain college \(60\%\) of the students are women and \(40\%\) are men but this time say it is \(50\%\) of the men working towards a math degree and \(25\%\) of the women. Do you expect the new count of math majors to be larger or smaller than the previous count?

 

Pedagogical Comment:

Students in grades K – 5 must develop a profound, intuitive, and flexible understanding of area.

Of course, they must first see a \(4 \times 6\) rectangle, for example, as a total of \(24\) unit squares arranged in a four-by-six array, and construct and draw and reflect on many examples like it.

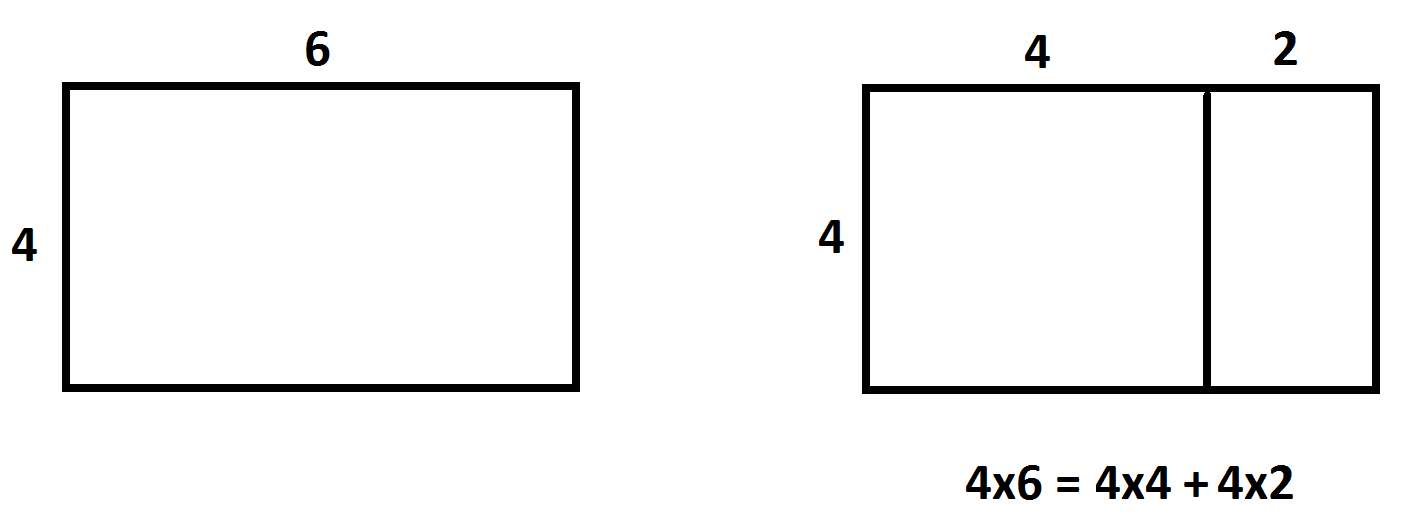
By folding or tearing paper, or by drawing lines across the entire figure, students should look for structure within these pictures, for example, to see \(4 \times 4 + 4 \times 2\) within \(4 \times 6\).

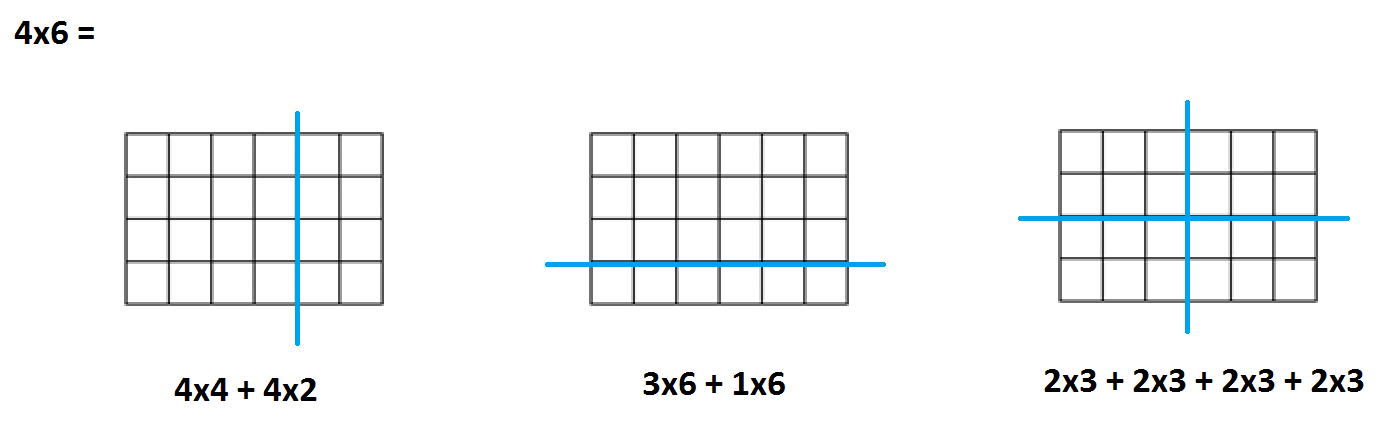
Eventually we must ease students away from the literal to work towards the conceptual, seeing a figure like the one below as still representing a rectangle of area \(24\) square units (without having to actually draw them in) and to play with the subdivided rectangle.

See the work of Geri Lorway for this. (Here are some more detailed notes: Click on Geri Lorways PDF .)

 

A FINAL COMMENT: 

I can’t help myself as a mathematician to comment on our opening, loose definition:

Loosely speaking, the area of a geometric figure is the amount of space inside it.

Yes, such a definition appeals to our intuitive understanding. But if we want to be precise with our definition we quickly become mired in deep conceptual haziness. What exactly do we mean by “amount” and by “space”? Even the word “inside” is problematic.

Exercise: We like to believe that every curve we draw in two-dimensional space divides space into two regions: a finite one called the inside of the loop and an infinite one called its outside. Is this obviously true? Does every curve drawn in the plane have this property? Does every loop drawn on the surface of the Earth have this property? (If so, what does “inside” mean?)

These are serious questions. If the Earth happened to be the shape of a donut, then there would be curves on planet that fail to divide the surface into two parts.

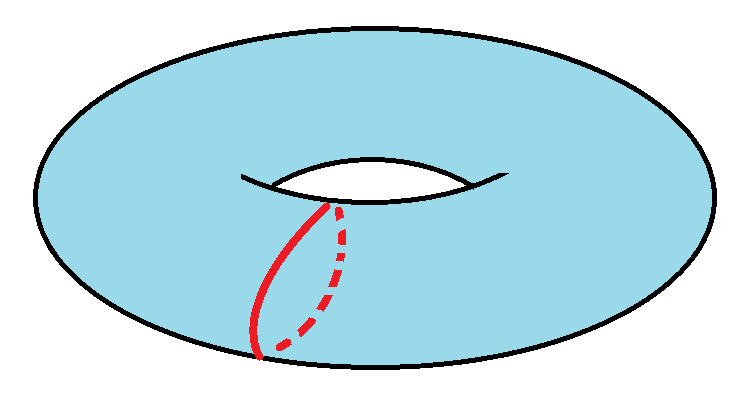
Of course the path out of this haziness is to follow the route we outlined in this lesson.

1. Declare first a value for the “area,” whatever that means, of a rectangle to be its length times width.

2. Next make two declarations about how “area,” whatever that means, should behave. We take the Area Addition Postulate and the Area Congruence Postulate.

3. Now follow the logical consequences of this opening declaration and the two stated beliefs.

This approach never answers the question as to what area truly is (nor ever settles what we mean by “space” and “amount of” and “inside”). And the whole issue developing an overarching definition has been completely side-stepped.  But because the opening declarations are based on our intuitive beliefs, the theory that follows seems to always match our intuition. That feels good and right.

(Now having said that, I should not mention the Banach-Tarski Paradox!)

 

Resources