Consider the traditional long multiplication algorithm. It is hard for us adults to look at it coldly because it is so familiar, but try for a moment to look at it from the perspective of a student seeing it for the first time. It is actually mighty strange:

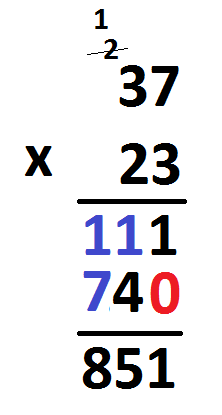
Some weird features:

Start from the right and work left. (We are taught to read left to right, so why not left to right now? Are all algorithms in mathematics in reverse order? Long division?)

Do ordinary multiplication of the single digits, but insert zeros along the way. Oh. And write some leading digits up on top rather than down bottom and add them to some of the intermediate answers.

Complete the multiplication by performing addition!

The natural burning question is:

What is the long multiplication algorithm really doing? Why does it work?

Comment: The form of long multiplication written above is very compact and is designed for the days when paper and ink were precious. A more transparent version of the long multiplication algorithm might today appear as:

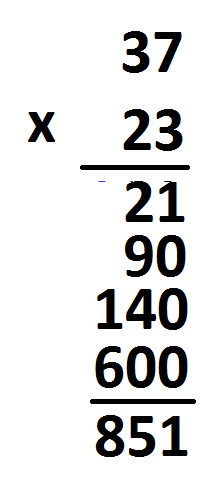
EXPLAINING THE ALGORITHM

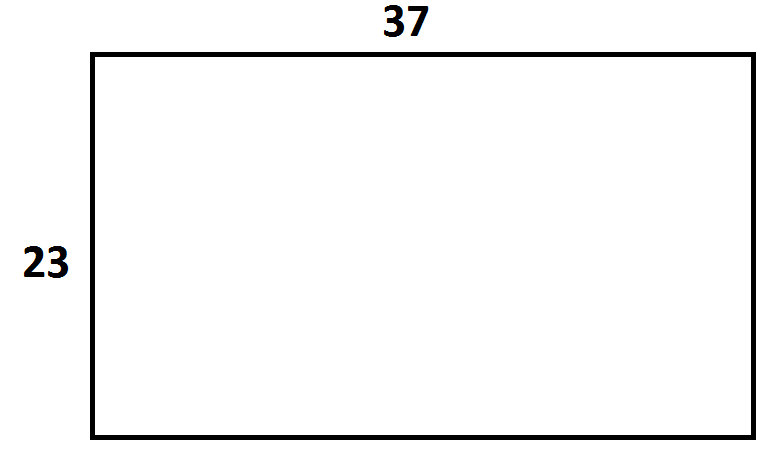
The geometric model of multiplication is area. Computing the product of two numbers is a computation of the area of a rectangle with side lengths those two values.

Thus \(37 \times 23\) corresponds to the area of a 37-by-23 rectangle.

It is compelling to divide this rectangle into convenient parts, compute the area of each piece, and add up individual areas. The computation \(37 \times 23=851\) is now absolutely apparent. (One can see this picture in one’s head and just do the work in there!)

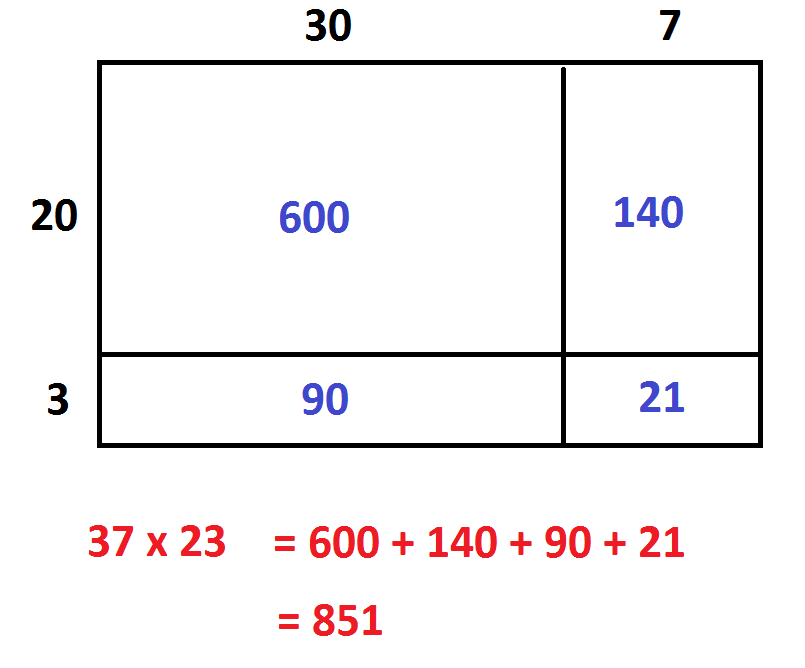
Moreover, explanation of the traditional algorithm is now clear. (Start with the less compact version of the algorithm, and then explain the shortcuts – using place-value carrying – with the more compact version.)

 

Exercise: What if we thought of \(37\) as \(10+10+10+7\) and \(23\) as \(10+10+3\) (as most students first want to do)? Draw the 37-by-23 rectangle subdivided into twelve pieces, compute the areas of the individual pieces, and verify that they have total sum \(851\).

 

Comment: I personally have no trouble with my students taking an extra three seconds to sketch rectangles in the margins of their pages when computing products.

 

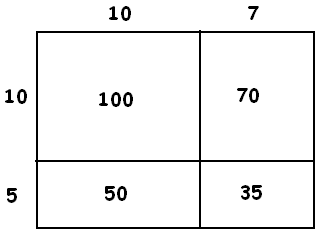
EXAMPLE: \(15 \times 17\).   

Answer: \(15 \times 17 = 100 + 70 + 50 + 35 = 255\).

 

EXAMPLE: \(371 \times 42\).

Answer: Subdivide a rectangle into six pieces.

\(371 \times 42 = \left(300+70+1\right) \times \left(40 + 2\right) = 12000 + 600 + 2800 + 140 + 40 + 2 = 15582\).

 

EXAMPLE: The computation \(\left(4+5\right)\left(3+7+1\right)\) corresponds to subdividing a rectangle into how many pieces?

Answer: Six pieces.

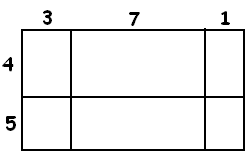
We have  \(\left(4+5\right)\left(3+7+1\right)=4 \times 3 + 4\times 7 + 4\times 1 + 5\times 3 + 5 \times 7 + 5 \times 1 = 12+28+4+15+35+5=99\).

Comment: This was a very complicated way of computing \(9 \times 11=99\)!

 

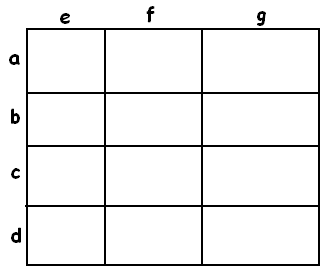
EXAMPLE: What does the computation \(\left(a+b+c+d\right)\left(e+f+g\right)\) mean geometrically?

Answer: It corresponds to subdividing a rectangle into 12 pieces.

With patience one could write this out:

\(\left(a+b+c+d\right)\left(e+f+g\right)=ae+af+ag+be+bf+bg+ce+cf+cg+de+df+dg\).

Comment:  One usually omits the multiplication sign “\(\times\)” or “\(\cdot\)” when multiplying two quantities represented by symbols.

 

ASIDE: ON THE STRANGENESS OF ALGORITHMS

Let me put you back in the place of a student by teaching you an algorithm for long multiplication that you might never have seen before. My job as a teacher is not to have you understand the algorithm, but to be able to perform and do well on a national assessment. Your job as a student is to practice the algorithm and to become fluent with it.

 

Here’s today’s lesson:

HOW TO DO LONG MULTIPLICATION:

We’ll illustrate the method with an example. Let’s compute \(22\times13\).

To do this, draw two sets of vertical lines, the left set containing two lines and the right set two lines (for the digits in \(22\) ) and two sets of horizontal lines, the upper set containing one line and the lower set three (for the digits in \(13\)).

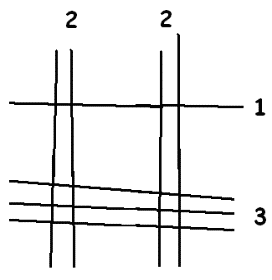
There are four sets of intersection points. Count the number of intersections in each and add the results diagonally as shown:

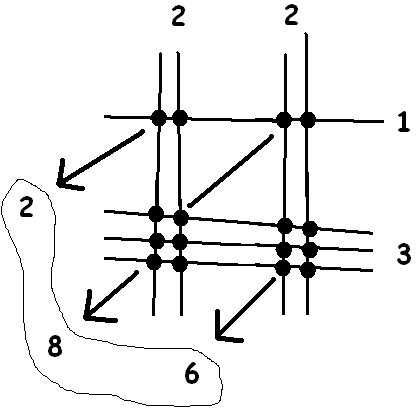
The answer \(286\)  appears.

 

There is one caveat as illustrated by the computation \(246\times 32\):

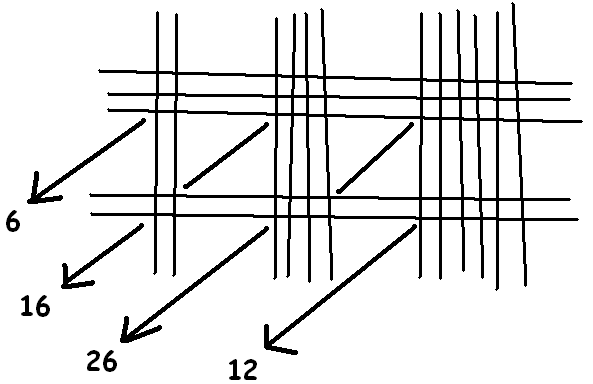
Although the answer 6 thousands, 16 hundreds, 26 tens, and 12 ones is absolutely correct, one needs to carry digits and translate this as 7,872.

 

PRACTICE:  Compute \(131\times 122\) via this method.

PRACTICE:  Compute \(54\times 1332\) via this method.

 

I’ll even be do my best as a teacher and give you something meaty to think about while teaching this algorithm and thereby meet a national problem-solving process standard.

 

CHALLENGE: How best should one compute \(102\times 30054\) via this method?

 

But, of course, the true burning question at hand is:  Why does this method work?

National assessments usually dictate classroom culture – turning the focus to speed answers to computation questions rather than slow mulling on “why?”, “what else?“, and “what if?” questions. All humans, even young ones, are curious and naturally want to know the whys and hows of things.

Resources