In the last lesson we computed \(23\times37\) via the area model:

\(23\times37=\left(20+3\right)\cdot\left(30+7\right)=20\cdot30+20\cdot7+3\cdot30+3\cdot7\)

 

Our work in expanding \(\left(20+3\right)\left(30+7\right)\) amounts to selecting one number from the first set of parentheses – 20 or 3 – and one number from the second set of parentheses – 30 or 7 – multiplying them together, and then adding all possible combinations of one number from each. Each individual product corresponds to the area of one piece of the subdivided rectangle.

 

The same work applies to larger products too. For example, in computing \(371\times42\) as \(\left(300+70+1\right)\left(40+2\right)\) we again select one term from each set of parentheses, compute their product, and sum all possible products formed this way.

\(\left(300+70+1\right)\left(40+2\right)=300\cdot40+70\cdot40+1\cdot40+300\cdot2+70\cdot2+1\cdot2\)

 

We saw a more abstract example in the last lesson too:

\(\left(a+b+c+d\right)\cdot\left(e+f+g\right)=ae+af+ag+be+bf+bg+ce+cf+cg+de+df+dg\)

 

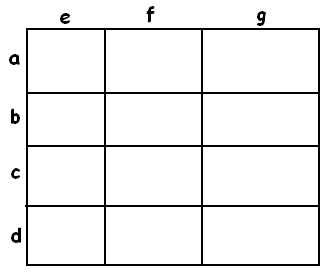
EXPANDING PARENTHESES (U.S.) / EXPANDING BRACKETS (U.K.)

To compute the product of two sums, select one term from each set of parentheses, multiply, and sum all possible products that could arise this way.

e.g. \(\left(a+b+c\right)\left(x+y+w+z\right)=ax+bx+cx+ay+\ldots\)

e.g. \(\left(a+b\right)\times c=ac+bc\)

e.g.\(\left(x+y\right)\left(p+q\right)=xp+yp+xq+yq\)

 

A comment on the DISTRIBUTIVE RULE: The second example above can be thought of the product of two sums within parentheses if we think of \(\left(a+b\right)c\) as \(\left(a+b\right)\left(c\right)\). Selecting one term from each set of parentheses corresponds to always choosing \(c\)  in the second set and so leads to the expansion: \(ab+ac\). This one single example, or its variant \(a\left(b+c\right)=ab+ac\) , is called the distributive rule in school textbooks.

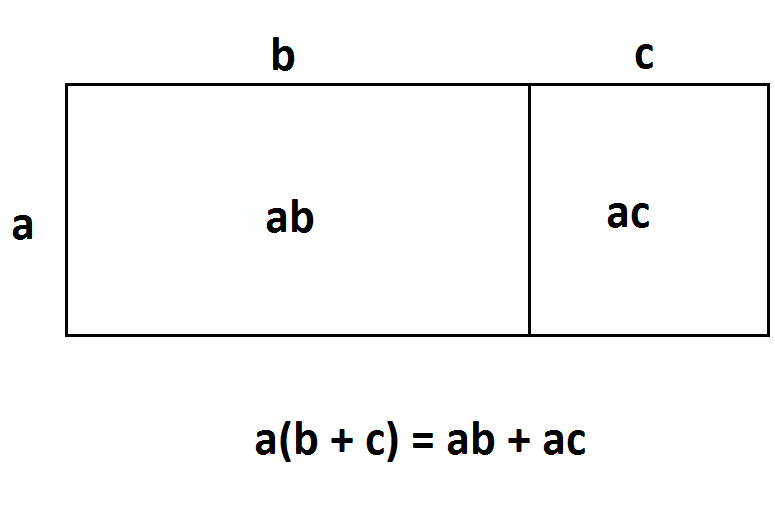
I personally do not think it is pedagogically helpful to single out this single example from the whole concept of expanding brackets. Mathematicians in advanced work have proven that all examples of expanding brackets follow logically from this one single rule, but that work, quite appropriately, is never shared with students. There is no reason in the student experience of mathematics to make this single example of expanding brackets special. Just expand all brackets!

 

A comment on FOIL (And why not LIFO and FLIO and OILF and ….?)

If you don’t know what this is, great! If you do know what this is, my adamant advice is to FORGET IT! It doesn’t help for expressions like \(\left(x+y+2\right)\left(a+b+c+7\right)\) .

It is much easier to always just expand brackets: selecting one term from each set of parentheses in turn, multiplying, and summing all possible products. This is far better than memorizing a special rule that works only for one specific type of example. (And students can figure out for themselves how to be systematic. Let them!)

EXERCISE: If you were to expand \(\left(x+y+2\right)\left(a+b+c+7\right)\) how many individual terms do you expect to see?

 

TAKING IT FURTHER … 

We have that \(\left(3+7\right)\left(4+5\right)\) corresponds to subdividing a rectangle into four pieces. So then …

 

What does \(\left(2+3\right)\cdot\left(4+5\right)\cdot\left(6+7\right)\) correspond to geometrically?

 

Think about this before reading on.

 

Answer:   \(\left(2+3\right)\cdot\left(4+5\right)\cdot\left(6+7\right)\) corresponds to dividing a three-dimensional block into EIGHT pieces.

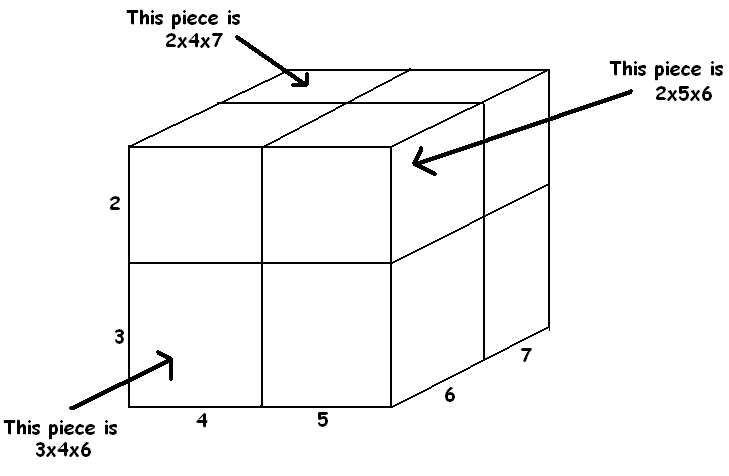
(Where is the  \(3\times4\times7\) piece in the picture?)

 

Here are the eight pieces listed out:

\(\left(2+3\right)\cdot\left(4+5\right)\cdot\left(6+7\right)\)

\(=2\times4\times6+2\times4\times7+3\times4\times6+3\times4\times7+2\times5\times6\)

\(+2\times5\times7+3\times5\times6+3\times5\times7\)

 

NOTICE AGAIN we are selecting one term from each set of parentheses and making sure to cover all possible combinations!

 

This example says that \(5\cdot9\cdot13=48+56+72+84+60+70+90+105\), which is indeed the case.

 

 

EXAMPLE: If one were to expand \(\left(x+y+z\right)\left(a+b+c+d\right)\left(r+s\right)\) how many terms would there be? What is happening geometrically?

Answer: There would be \(3\times4\times2=24\) terms. (Do you see why?) The expression corresponds to subdividing a rectangular block into 24 pieces.

 

EXERCISE 1: If one were to expand \(\left(x+y\right)\left(x+a+b\right)\left(a+c+p\right)\) 

a) how many terms would there be?

b) would \(xac\) be one of those terms? How about \(cay\) ? \(xcp\) ? \(x^{2}a\) ? \(axy\) ? \(xyc\) ?

(Answers appear at the end of this lesson)

 

EXERCISE 2: If one were to expand this expression

\(\left(a+b+c+d+e\right)\left(w+x\right)\left(a+x+b+t+r\right)\left(e+f\right)\)

how many terms would there be?  Is there a geometric interpretation to this expression?

 

EXERCISE 3: WITHOUT A CALCULATOR compute:

a) \(24\times14\)

b) \(106\times 21\)

c) \(213\times31\)

(As an example, \(13\times26=\left(10+3\right)\left(20+6\right)=200+60+60+18=338\).)

Try to do these in your head!

 

EXERCISE 4: One can compute \(\left(2+3\right)\cdot\left(7+4\right)\) two ways:

Short way: \(\left(2+3\right)\cdot\left(7+4\right)=5\cdot11=55\)

Long way: \(\left(2+3\right)\cdot\left(7+4\right)=2\cdot7+2\cdot4+3\cdot7+3\cdot4\)

Compute each of the following both the short way AND the long way.

a) \(\left(2+3\right)\cdot\left(3+7\right)\cdot\left(1+5+5\right)\)

b) \(\left(2+4+6\right)\cdot\left(2+6+1+3\right)\)

 

ASSOCIATIVE LAW FOR MULTIPLICATION

As a final comment, we should point out that many people feel that three-dimensional thinking justifies the associative law for multiplication:

 

\(\left(ab\right)c=a\left(bc\right)\) for all counting numbers \(a\), \(b\), and \(c\).

 

Can you see how computing the volume of the following solid two different ways justifies this belief? (Maybe there is a little commutativity thinking going on too!)

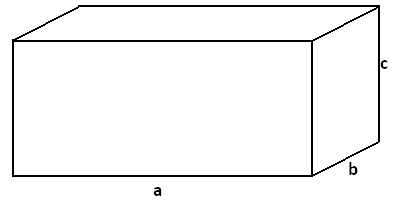
Exercise Answers:

1. a) There will be \(2\times3\times3=18\) terms.

b) All the terms listed but one do appear: \(xcp\) does not appear.  (Note: The terms that appear might do so with a different order for their product: \(cay\) might appear as \(yac\), for instance.)

2. There will be \(5\times 2\times 5\times 2=100\) terms. I am personally not sure how to draw a four-dimensional block and show it subdivided into pieces. But I do feel sure the mechanics of the matching algebra will be the same.

3. \(24\times 14 = \left(20+4\right)\left(10+4\right)=200+40+80+16=336\).

\(106\times 21=\left(100+6\right)\left(20+1\right) = 2000+120+100+6=2226\).

\(213\times31 = \left(200+10+3\right)\left(30+1\right)=6000+300+90+200+10+3=6603\).

4. The short ways give \(5\times10\times11=550\) and \(12\times12=144\). One can check that the long ways do too!

 

 

 

 

 

 

Resources