Here is a story that isn’t true.

When I was a young child I used to spend my days sitting in a sandbox at the back of my yard (not true). And being a very Zen-like child (definitely not true!) I started each day leveling the sand to make a perfectly flat horizontal surface. This very much appealed to my tranquil sensibilities – so much so that, in fact, I decided to give this level state of perfection a name. I called it the “zero” state and denoted it \(0\).

I spent many an hour admiring my zero state (still not true). But then, one day, I had an epiphany! I realized I could reach behind where I was sitting, grab a handful of sand, and make a pile. I called the one pile the “one” state, denoting it \(1\).

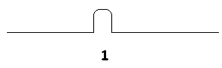
Next I discovered two piles, which I called “2,” and three piles, “3,” and so forth.

Hours of mathematical fun were had as I discovered the counting numbers with piles of sand and their arithmetic:

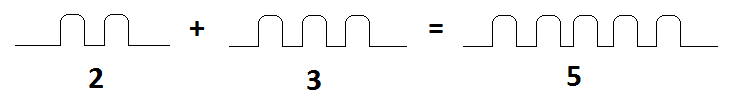
BUT THEN … one day I had the most astounding epiphany of all! Instead of using a handful of sand to make a pile, I could, I realised, take away a handful of sand and make the OPPOSITE of a pile, namely, a hole. Whoa!

 

I denoted this “opp 1” for the opposite of one pile noticing that “opposite,” in some sense, is really the right word since a hole cancels a pile:

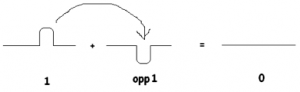
\(1 + opp 1 = 0\)

 

In the same way “opp 2” represents the opposite of two piles, namely, two holes, and “opp 5” the opposite of five piles, namely, five holes.

Exercise 1: Draw a picture for \(2 + opp 2\) and explain why it too equals zero.

Exercise 2: a) Daphne says that \(3 + opp 2\) equals one pile. She is correct.  Draw a picture to demonstrate.  b) Harold says that \(5  + opp 7\) equals \(2\) holes. Is he correct? Draw a picture. 

 

I realised, too, that the opposite of a hole is a pile.

 

Exercise 3: a) What is the opposite of the opposite of a hole? 

b) What is the opposite of the opposite of the opposite of three piles?

 c) What is the opposite of the opposite of the opposite of the opposite of the opposite of the opposite of the opposite of the opposite of the opposite of the opposite of the opposite  of the opposite of the opposite of ten hundred holes?

 

This untrue story shows how I allegedly discovered as a young child the counting numbers and their opposites. The world calls the opposite of a counting number a negative number. And instead of writing opp for opposite, people use a tiny dash “-“. So

Unfortunately, matters become a little confusing when one starts combining piles and holes.  For example, three piles and two holes together (giving one pile) is written: \(3 + \; – 2 = 1\).

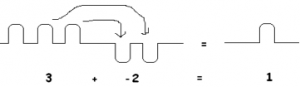
and \(5 + \; – 7 = -2\) is a clunky way of writing “five piles and seven holes equals two holes.”

 

 

Exercise 4: a) Alistaire invented notation that looks as follows: \(4P + 5H + 3H + 2P = 2H.\) What do you think he means by this? Do you like his notation? 

 b) Cuthbert writes: \(\bar{3} + \underline{4} + \bar{5} = \bar{4}\) . What do you think he means by his notation?

 

Exercise 5: The statement: 

\(-3+7=4\) 

reads “3 holes and 7 piles makes 4 piles,” and the statement:

 \(17+\;-6+\;-4+6+\;-20=-7\)

reads “17 piles and 6 holes and 4 holes and 6 piles and 20 holes makes 7 holes.”

Translate each of the following into the language of piles and holes, and give the answers.

a) \(5+\;-9+2\)

b) \(3+\;-10+11+\;-5\)

c) \(2+\;-2+2+\;-2+2+\;-2\)

d) \(-6+\;-1+\;-2+\;-3\)

 

Exercise 6: Pandi writes: 

\(- – – – – – 5+ – – 2+ – – – – 3+ – – – – – – – 8\) 

This actually makes sense! What does it mean and what is the answer?

  

Many educators will not let students write, for example,

\(5+\:-7=-2\)

as most of the world prefers to phrase everything in terms of subtraction. In fact, early grade students are first taught subtraction, reading \(5-2\) as “five take away two.” But it is really

 \(5+-2\)

that is, “five piles plus the ADDITION of two holes.” Of course, adding two holes has the same effect as taking away two piles:

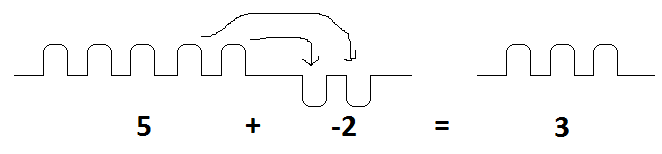
As another example,  \(6-4+1\) is usually read as “six take away four plus one.”  It is equivalently

 \(6+-4+1\)

that is, “six piles PLUS four holes PLUS one pile” which is three piles.

 

Comment:  Young children naturally ask about subtraction problems like \(3-5=?\) and \(1-4=?\) and are sometimes told that these problems just don’t have answers. But at some point it pedagogically appropriate to open up the world of number thinking and introduce piles and holes. In fact, mathematicians would argue that in the theoretical context of arithmetic:  

Subtraction does not really exist.  SUBTRACTION is just the ADDITION of opposites.

Encouraging this change of thinking for middle-school students has profound effect one their work and thinking algebra classes!

 

 

ON “DISTRIBUTING THE NEGATIVE SIGN”

Here’s a vague question: What is the opposite of three piles and two holes? Does this mean the opposite of three piles AND THEN the addition of two holes or the opposite of BOTH three piles and of two holes?

Mathematicians, of course, use parentheses to help clarify such confusion. Parentheses group objects together. Examples explain.

 

EXAMPLE:  \(-\left(3+\;-2\right)\).

This means the opposite of everything in the parentheses, that is, the opposite of BOTH three piles and two holes. And what is the opposite of both three piles and two holes? Clearly, three holes and two piles: \(-\left(3+\;-2\right)=-3+2\).

This is one hole.

\(-\left(3+\;-2\right)=-3+2=-1\).

 

Comment: In terms of subtraction this reads:  \(-\left(3-2\right) = -3+2=-1\) . It really is conceptually easier to think in terms of piles and holes.

 

EXAMPLE: \(-\left(3+\;-4+2\right)+5\).

This is the opposite of all of \(3\) piles, \(4\) holes and \(2\) piles, AND THEN the addition of \(5\) piles. So we have \(3\) holes, \(4\) piles, \(2\) holes, and \(5\) piles. This is, in all, \(3\) piles.

\(-\left(3+\;-4+2\right) + 5 = -3 + 4 + -2 + 5 \).

Comment: In terms of subtraction this reads:  \(-\left(3-4+2\right) + 5 = -3 + 4 + -2 + 5 \) .

 

EXAMPLE: \(6-\left(5-2\right)\).

This is \(6\) piles and the opposite of both \(5\) piles and \(2\) holes: \(6-\left(5-2\right) = 6 + \;-5 + 2\).  (And this equals \(3\) piles if you are interested in answers.)

 

EXAMPLE: \(\left(5-2+1\right) – \left(3-2\right) \).

This is \(5\) piles, \(2\) holes and \(1\) pile all grouped together PLUS the opposite of both \(3\) piles and \(2\) holes.

\(\left(5-2+1\right) – \left(3-2\right) = 5 + \;-2 + 1 + \;-3 + 2.\)

 

EXAMPLE: \(10 + \left(5-8\right) \). 

This is \(10\) piles PLUS a group of \(5\) piles and \(8\) holes:

\(10 + \left(5-8\right) = 10 + 5 + \;-8 \).

 

Comment: All these examples are illustrating the process of “distributing the negative sign (and the plus sign!)” If you think piles and holes, it is all a non-issue.

 

Exercise 7: Interpret and evaluate each of the following: 

a) \(6-\left(3-2\right) \)

b) \(4+\left(1-3\right) \)

c) \( \left( 3-9-1\right) – \left(8+2\right)\)

d) \(\left(1+2-4\right) – \left(3+2-4\right) \)

e) \( \left(2-3\right) – \left (5-2-3+7\right) – \left(-9+8-1\right) + \left(-2-3\right) \)

f) \(\left( 16-16\right) – \left(17-17\right) \)

 

Exercise 8:  (A great exercise for algebra students!)  What is \(-x\) if:

a)  \(x\) is seven piles?

b)  \(x\) is seven holes?

c)  \(x\) is \(50\)?

d)  \(x\) is \(-50\)?

 

Exercise 9:  Wanda is thinking of a number, which she calls \(W\), but she refuses to tell us its value. But she does ask us to compute:

\(\left(4-W\right) – \left(2-W\right)\)

Without knowing her number do we have any chance of working this out?

 

EXAMPLE: Make the expression \(2-\left(20-x\right)\) look simpler.

Answer: Two piles and the opposite of “20 piles and \(x\) holes” is two piles and 20 holes and \(x\) piles:

\(2-\left(20-x\right) = 2+\; -20+x=\:-18+x=x-18\).

 

ADVENTURE: CARD PILE TRICK

a)    Take \(10\) red cards and \(10\) black cards from a deck of cards. Shuffle your \(20\) cards and arbitrarily split them into two equal piles. Count the number of red cards in the left pile and the number of black cards in the right pile. What do you notice? Repeat this activity two more times.

b)    Shuffle your \(20\) cards and this time split them into a pile of \(6\) and a pile of \(14\) cards. Count the number of red cards in the small pile and count the number of black cards in the large pile. Take the (positive) difference of those two counts. Did you get \(4\)? Repeat this two more times.

c)    Shuffle the \(20\) cards again and this time split them into a pile of \(9\) cards and a pile of \(11\) cards. Count the number of red cards in the small pile, count the number of black cards in the large pile and take the (positive) difference of this count. What did you get? Repeat two more times. What do you notice?

d)    Complete the following table:

 

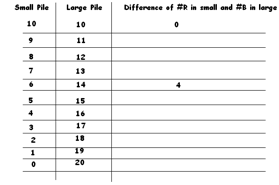
Any patterns?

e)    Suppose, in a game with \(5\) cards in the small pile and \(15\) cards in the large pile, I counted three red cards in the small pile. Complete the following table:

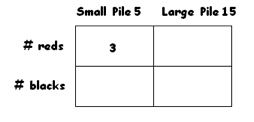
What is the difference of counts of red cards in the small pile and black cards in the large pile?

f)   Suppose the small pile again has 5 cards and the large pile has 15 cards. Suppose it turns out there are \(R\) red cards in the small pile. Complete the following table as an abstract exercise, writing formulas in each cell of the table solely in terms of \(R\):

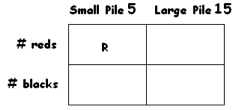
What can you say about the difference between the number of red cards in the small pile and the number of black cards in the large pile?

Does this match what you observed in part d) of this question? 

g)  Call the number of cards in the small pile \(P\) and the number of cards in the large pile \(20-P\). (Why is this the correct formula for this?) Suppose there are \(R\) red cards in the small pile. Complete the table again as the ultimate abstract exercise, writing formulas in each cell of the table solely in terms of \(P\) and \(R\):

Can you write a formula for the difference of counts of the red cards in the small pile and black cards in the large pile? Does this formula match the data you obtained in part d) of this question?

 

THE CLASSIC MILK AND SODA PUZZLE

Saku has a glass of soda and a glass of milk. She takes a tablespoon of soda from the first glass and haphazardly stirs it into the milk. She then takes a tablespoon of the milk/soda mixture and transfers it to the soda. Both drinks are now “contaminated.”

Here’s the question: Which has more foreign substance? Is there more foreign milk in the soda than foreign soda in the milk? Is it the other way round? Or is it impossible to say?  

COMMENT: Part a) of the previous activity can be thought of as a “ten molecule” version of this puzzle.

 

Answers to Select Exercises:

3. a) One hole  b) \(3\) holes  c) ten hundred piles

4. a) \(P\) stands piles and \(H\) stands for holes.   b) Over-bar stands for piles and under-bar for holes. (Or could it be the other way around and still be consistent?)

6. \(5+2+3-8=2\).

7. a) \(6-3+2=5\)

b) \(4+1-3=2\)

c) \(3-9-1-8-2=-17\)

d) \(1+2-4-3-2+4=-2\)

e) \(2-3-5+2+3-7+9-8+1-2-3=-11\)

f) \(16-16-17+17=0\)

8. a) Seven holes   b) Seven piles  c) \(-50\)  d) \(50\)

9. \(4-W-2+W=2\)

MILK AND SODA: Pull out the contaminant from the soda leaving a space. Where is the missing soda that once filled that space?

Resources